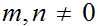 be two integers. There exits unique integers
be two integers. There exits unique integers
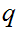 and
and
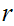 with
with
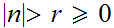 and
and
Let
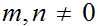 be two integers. There exits unique integers
be two integers. There exits unique integers
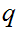 and
and
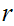 with
with
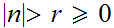 and
and
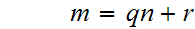
Uniqueness follows from the fact that
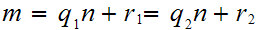 implies
implies
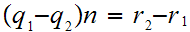 thus assuming
thus assuming
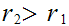 we have
we have
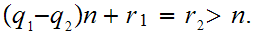
Let
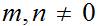 be two integers. The greatest common divisor of
be two integers. The greatest common divisor of
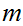 and
and
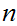 is defined to be largest integer
is defined to be largest integer
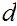 such that
such that
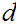 divides both
divides both
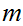 and
and
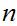 . We write
. We write
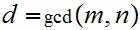 .
.
Since
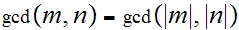 one can effectively , thought very inefficiently, compute
one can effectively , thought very inefficiently, compute
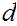 by dividing by all values, starting at
by dividing by all values, starting at
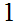 and ending at the least of
and ending at the least of
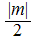 and
and
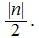
Examples:
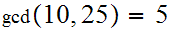 .
.
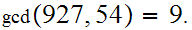
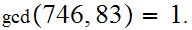
Suppose
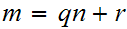 then
then
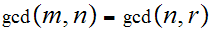 .
.
If
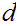 divides both
divides both
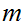 and
and
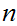 it also divides both
it also divides both
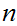 and
and
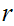 thus the two pair have exactly the same set of common divisors!
thus the two pair have exactly the same set of common divisors!
Let
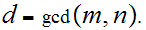 Using the Algorithm described in the proof below, there exists effectively
computable integers
Using the Algorithm described in the proof below, there exists effectively
computable integers
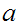 and
and
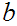 such that
such that
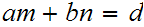
If
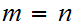 the theorem is trivial so for simplicity assume that
the theorem is trivial so for simplicity assume that
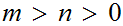 .
Again if
.
Again if
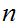 divides
divides
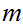 the theorem is trivial so assume
the theorem is trivial so assume
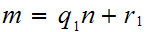
 with
with
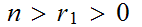 .
.
By the lemma
above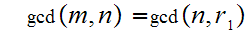
If
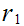 divides
divides
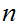 then
then
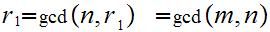 and
and
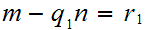 .
.
Otherwise
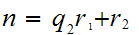
 with
with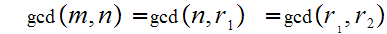
Again if
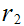 divides
divides
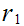 ,
,
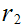
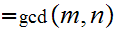 and and by substitution we have
and and by substitution we have
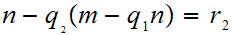 or
or
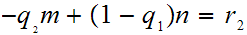
By induction,we have
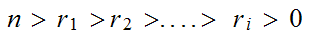
and
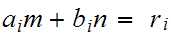
One finally argues that after at most
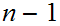 steps
steps
 since
if
since
if
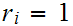 it is the greatest common
divisor.
it is the greatest common
divisor.
Let
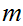 ,
,
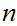 ,
and
,
and
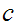 be integers, then the equation
be integers, then the equation
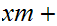
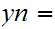
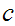 has integer solutions if and only if
has integer solutions if and only if
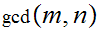 divides
divides
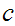 .
.
PROOF:.
If
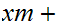
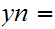
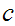 ,
any common divisor of
,
any common divisor of
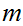 and
and
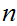 , in particular
, in particular
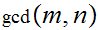 ,
must divide
,
must divide
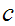 .
.
If
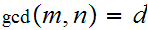 and
and
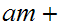
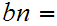
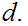 Let
Let
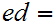
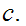 Then
Then
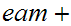
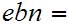
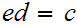
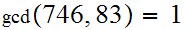
Applying the Euclidean Algorithm,
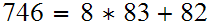
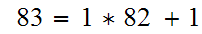
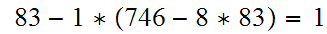
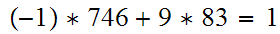
Homework Due (Nov 3):
Estimate the number of divisions that it takes to compute
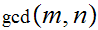 using
the Euclidean Algorithm .
using
the Euclidean Algorithm .
hint: Assume that
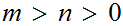 ,
,
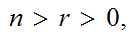 and
and
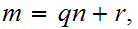 show
show
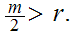
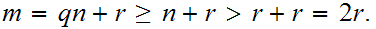
The Steps in the Euclidean Algorithm:
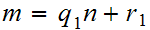
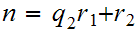
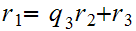
.
.
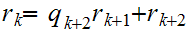 with
with
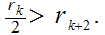 or
or
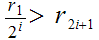
Let
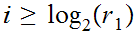 then
then
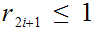 so
so
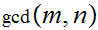 can be computed in at most
can be computed in at most
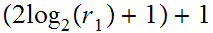
steps. The first step being the computation of
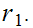
Finally, in terms of
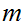 and
and
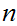 ,
,
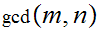 can be computed in at most
can be computed in at most
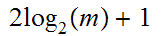
Suppose
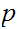 is prime . Suppose
is prime . Suppose
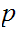 divides
divides
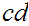 then
then
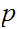 divides
divides
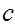 or
or
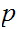 divides
divides
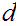 .
.
Proof:
If
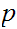 does not divide
does not divide
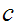 ,
then
,
then
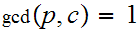 .
Thus there exists integers
.
Thus there exists integers
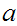 and
and
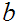 , such that
, such that
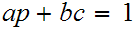
Multiplying both sides of the equation by
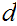 we have
we have
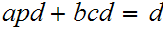
Since, by assumption,
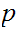 divides
divides
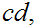 both terms on the left hand side are divisible by
both terms on the left hand side are divisible by
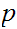 , hence, so is the right hand side.
, hence, so is the right hand side.
1. Let
 be a natural number then there is a unique set of prime numbers
be a natural number then there is a unique set of prime numbers
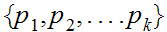 and natural numbers
and natural numbers
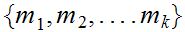 such that
such that
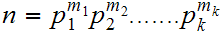
2. Every fraction
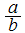 can be uniquely written as
can be uniquely written as
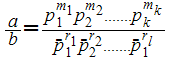 such that
such that
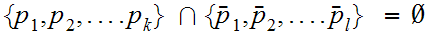
1. is a straight forward induction argument using 21.5. Given 1., 2. is immediate
There does not exist a rational number
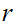 such that
such that
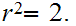
PROOF:.
Let
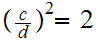 .
Applying 21.6.2. above we may assume
.
Applying 21.6.2. above we may assume
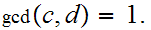 Multiplying, we have
Multiplying, we have
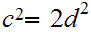 .
Since
.
Since
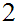 divides
divides
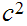 we conclude from 21.5 above that
we conclude from 21.5 above that
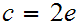 for some
for some
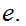
Hence
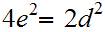 or
or
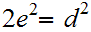 .
Hence as before
.
Hence as before
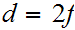 .
Thus
.
Thus
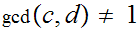 .
.