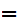 y
y

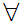 z
(z
z
(z x
x
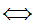 z
z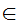 y
y
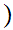 .
.
We start with A Brief History of Set Theory
Axiom ZF1 - Sets with the same members are equal - (Extensionality).
If x and y are sets then x
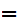 y
y

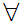 z
(z
z
(z x
x
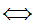 z
z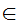 y
y
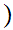 .
.
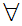 x
x
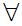 y
y
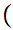 x
x
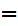 y
y
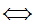
 z
(z
z
(z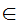 x
x
 z
z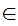 y
y
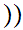
Axiom ZF2 - The "Empty Set" is a set. We write it as

There exists a set
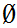 such that
such that
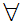 x(
x(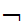 (x
(x
 )).
)).
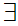 y
y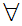 x(
x(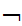 (x
(x
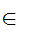 y))
y))
Note by ZF1
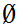 is unique.
is unique.
Axiom ZF3 - Set Formation - Unordered Pairs.
If x,y are sets then there exists a set z such that
 a
a
 a
a z
z
 a
a
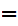 x or a
x or a
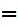 y
y
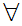 x
x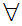 y
y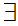 z
z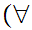 a
a
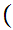 a
a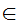 z
z

 a
a
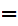 x or a
x or a
 y
y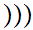 .
.
Notation: We write this unique set as {x,y} . Note that {x,x} which is the same as {x} is not the set x.
Axiom ZF4 - Set Formation - Union.
If x is a set then there exists a set y such that
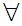 a
a
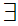 y
y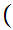 a
a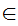 y
y
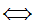
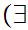 z
z z
z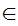 x
and
a
x
and
a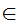 z
z
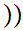 .
.
Notation: We
write y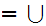 x
, or some variant thereof
x
, or some variant thereof
Axiom ZF5 - Set Formation - Power set.
If x is a set then there exists a set z such that
 y
y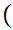 y
y z
z
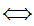 y
y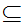 x
x
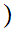 .
.
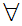 x
x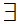 z
z y
y
 y
y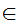 z
z
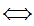
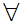 a
(a
a
(a y
y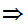 a
a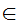 x
) )
x
) )
Notation:
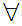 a
(a
a
(a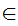 y
y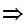 a
a x
) is just a definition of
inclusion y
x
) is just a definition of
inclusion y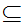 x
x
Axiom ZF6 - Set Formation - Selection.
If z and
 x
x is a proposition then there exits a set y such that
is a proposition then there exits a set y such that
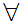 x(x
x(x y
y

 x
x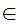 z
and
z
and
 x
x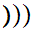 .
.
 z
z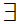 y
y x
x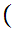 x
x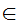 y
y

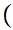 x
x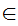 z
and
z
and
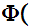 x
x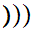 .
.
Note that this avoids Russell's Paradox since we require x to be a member of a "known Set."
Notation:We write
y x
x z
z
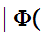 x
x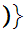 .
.
Axiom ZF7 - There is an infinite Set
There exists a Set m such that
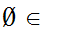 m
and
m
and
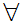 x
x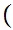 x
x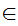 m
m
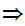
 x
x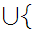 x
x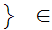 m
m .
.
 m
m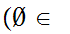 m
and
m
and
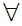 x
x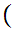 x
x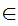 m
m
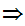
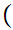 x
x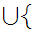 x
x m
m
Translation: x
x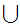 {x}
is the Set containing all the members of x and the Set
x itself.
{x}
is the Set containing all the members of x and the Set
x itself.
A Computation:
Step:0
 m
m
This Set has zero members.
1 m
m
Since
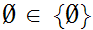 ,this set has one member, the Set with 0 members.
,this set has one member, the Set with 0 members.
2 m
m
This set has two members, the Set with 0 members, a Set with 1 member.
3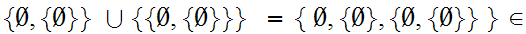 m
m
This set has three members, the Set with 0 members, a Set with 1 member and a Set with 2 members.
.
.
n
ZF7 allows us to "construct" the natural numbers.
Axiom ZF8 - Replacement( Functional Image)
Let
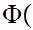 x
x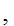 y
y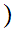 be
a proposition.
be
a proposition.
Suppose 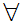 x
x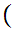
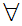 y
y y
y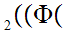 x
x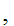 y
y and
and
 x
x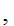 y
y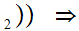
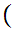 y
y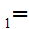 y
y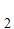
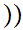
That is,
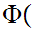 x
x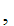 y
y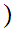 is a "single valued function."
is a "single valued function."
then
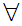 a
a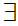 b
b c
c 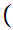 c
c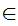 b
b

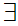 d
d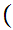 d
d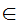 a
and
a
and
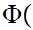 d
d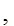 c
c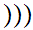
Translation: The functional image of a Set is a Set.
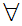 x
x
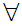 y
y y
y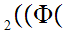 x
x y
y and
and
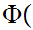 x
x y
y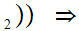
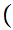 y
y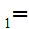 y
y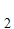
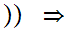
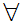 a
a b
b c
c  c
c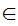 b
b
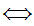
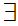 d
d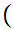 d
d a
and
a
and
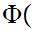 d
d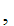 c
c
Axiom ZF9 - There are not Russell's Paradox like Sets (Regularity).
If x is a set and x
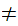
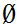 then
then
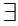 y
y
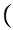 y
y x
and
x
and
 a
a
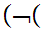 a
a x
and
a
x
and
a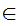 y
y .
.
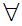 x
x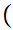 x
x
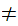
 y
y
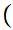 y
y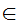 x
and
x
and
 a
a
 a
a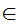 x
and
a
x
and
a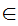 y
y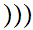
Translation: Every non-empty set contains a member that does not any members in common with it.
Note
 a(
a(
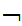 (a
(a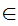 x
and
a
x
and
a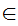 y)).
can be read
x
y)).
can be read
x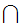 y
y .
This can be shown to rule out the Russell set.
.
This can be shown to rule out the Russell set.