 is said to be partially ordered or a poset if there is a binary relation
"
is said to be partially ordered or a poset if there is a binary relation
" "
defined on
"
defined on
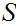 such that
such that
.
Definitions and Notation:
Reviewing, A set,
 is said to be partially ordered or a poset if there is a binary relation
"
is said to be partially ordered or a poset if there is a binary relation
" "
defined on
"
defined on
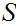 such that
such that
For all

For all
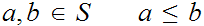 and
and
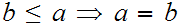
For all
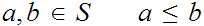 and
and
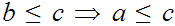
We will use the notation
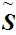 to represent the pair
to represent the pair
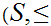
 .
.
Remember a chain in a poset
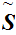 to be a totally ordered subset
to be a totally ordered subset
 .
That is for any
.
That is for any

 or
or
 .
We introduce the notation
.
We introduce the notation
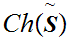 for
the subset of chains of
for
the subset of chains of
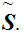 We also introduce the notation
We also introduce the notation
 for
the Well Ordered chains
for
the Well Ordered chains
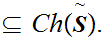
Given
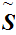 , let
, let
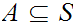 An element
An element
 is called an upper bound for
is called an upper bound for
 if
if
 for
all
for
all
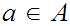 . Suppose also that
. Suppose also that
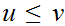 for all upper bounds
for all upper bounds
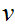 of
of
 then
then
 is called the least upper bound (l.u.b.). Define
lower bound and greatest lower bound
(g.l.b.) is a similar manner. We will sometimes also use the
notation,
is called the least upper bound (l.u.b.). Define
lower bound and greatest lower bound
(g.l.b.) is a similar manner. We will sometimes also use the
notation,
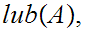 and
and
 .
.
If
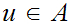 is also an upper bound for
is also an upper bound for
 then it is called the top element of
then it is called the top element of
 .
Note that being the top element implies uniqueness and that it is the least
upper bound. Define the bottom element similarly.
.
Note that being the top element implies uniqueness and that it is the least
upper bound. Define the bottom element similarly.
Finally,
Let
 be a given set. We also introduce the notation
be a given set. We also introduce the notation
 for the Set of subsets of
for the Set of subsets of
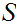 One verifies that
One verifies that
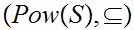 is a poset . Note that any
is a poset . Note that any
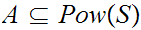 has a least upper bound and a greatest lower bound given be set union and
intersection,
has a least upper bound and a greatest lower bound given be set union and
intersection,
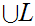 and
and
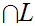 .
.
Definitions: A poset
(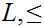 )
is called a "lattice" if every pair of elements
)
is called a "lattice" if every pair of elements
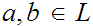 has a l.u.b., written
has a l.u.b., written
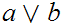 and a g.l.b., written
and a g.l.b., written
 .
Note that this implies that any finite set of elements has a g.l.b. and l.u.b.
Why?
.
Note that this implies that any finite set of elements has a g.l.b. and l.u.b.
Why?
Note that, trivially

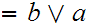 and
and
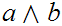
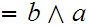
A lattice is complete if every subset
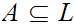 has a l.u.b. and a
g.l.b.(
has a l.u.b. and a
g.l.b.(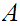 may be infinite!)
may be infinite!)
A lattice is distributive if
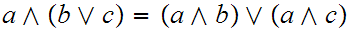 and
and
 for all
for all
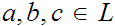 .
.
A lattice is complemented if
it has a top and bottom elements
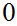 and
and
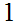 .
.
for every
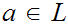 there is an element
there is an element
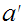 such that
such that
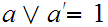 and
and
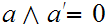 .
Check that
.
Check that
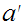 is unique
in a complemented distributive lattice.
is unique
in a complemented distributive lattice.
A complemented distributive lattice is called a Boolean algebra.
Examples of Boolean algebras:
The algebra of subsets of a given Set.
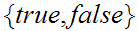 ,under
the usual rules of logic.
,under
the usual rules of logic.
n-bit binary words. ("computer logic")