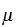 (called
a measure),
(called
a measure),
Does there exist a function
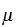 (called
a measure),
(called
a measure),
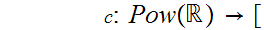 0
0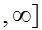
such that
0
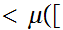 0,1
0,1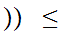 1
1
For all
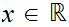 and
and
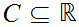 ,
,
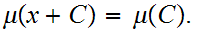
If
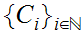 is a countable, pairwise disjoint, Set of subsets of
is a countable, pairwise disjoint, Set of subsets of
 then
then
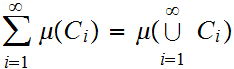
?
The answer is no! We will show this by producing
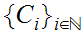 a countable, pairwise disjoint Set of subsets such that
a countable, pairwise disjoint Set of subsets such that
 0,1
0,1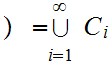
and
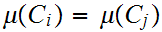 for all
for all
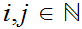
Hence 1. and 3. cannot hold simultaneously.
The construction of
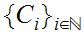
All contructions will be assumed to take place in
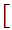 0,1
0,1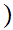 .
In particular,
.
In particular,
For 0
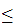
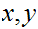
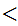 1,addition will be
1,addition will be
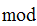 1
1
and on this Page
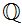 will denote the rational numbers in
will denote the rational numbers in
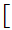 0,1
0,1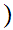 .
.
Exercise: Verify that
If
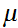 is translation invariant, it is also translation
is translation invariant, it is also translation
invariant with respect to addition
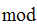 1.
1.
It suffices to show that there is a Set
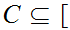 0,1
0,1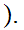
such that
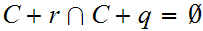 for any
for any
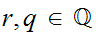 and
and
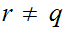 .
.
and
 0,1
0,1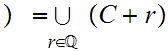
The construction of
Define and equivalence relation on
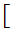 0,1
0,1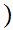 by setting
by setting
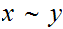 if
if
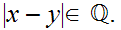
Let
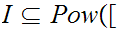 0,1
0,1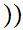 be the Set of equivalence classes.
be the Set of equivalence classes.
Invoking the Axiom of Choice on
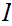 ,
Let
,
Let
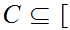 0,1
0,1 be any "Choice Set."
be any "Choice Set."
Specifically for any
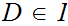 ,
,
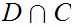 contains a single member.
contains a single member.
Note that
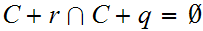 for any
for any
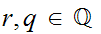 and
and
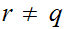
since if
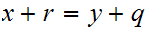 for
for
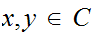 and
and
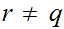
then
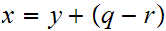 in particular
in particular
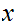 and
and
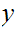 are
in the same equivalence class so
are
in the same equivalence class so
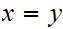 .
.