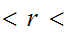 1,
, written
1,
, written
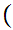 0,1
0,1 .
.
Since we are particularly interested in the cardinality of the Reals, it turns
out to be notationally simpler to work with the "open" unit interval
0 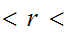 1,
, written
1,
, written
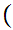 0,1
0,1 .
.
9.5 Lemma
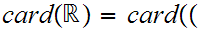 0,1
0,1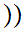
Proof:
This amounts to producing the appropriate 1 to 1
onto map of Dedekind cuts.
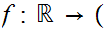 0,1
0,1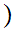 .
For clarity, this can be done as a composition,
.
For clarity, this can be done as a composition,
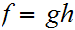
 -1,1
-1,1 where
where
 x
x

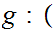 -1,1
-1,1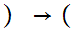 0,1
0,1 where
where
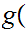 x
x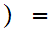
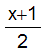
We will want to calculate the cardinality of the Continuum of Real Numbers. We
begin by identifying the set of Dedekind cuts in
 0,1
0,1 with
a particular set of infinite decimal fractions. Explicitly,
with
a particular set of infinite decimal fractions. Explicitly,
Let
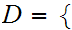 0,1,2,3,4,5,6,7,8,9
0,1,2,3,4,5,6,7,8,9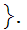 Note
that applying 9.4,
gives
Note
that applying 9.4,
gives 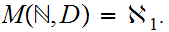
Let
 be all maps not excluded by the following two bullets.
be all maps not excluded by the following two bullets.
The constant map
 x
x 9
is not in
9
is not in
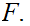
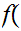 x
x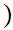 is not in
is not in
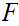 if there exists an n such that
if there exists an n such that
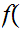 x
x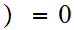 for all x
for all x
 n.
n.
Notationally, given
 we write
we write
 i
i d
d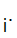 We are identifying
We are identifying
 with the infinite
with the infinite
decimal fractions,
.d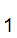 d
d d
d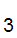 ......d
......d .....
.....
Where not all the
d 9
and the sequence does not end in an infinite string of 0's.
9
and the sequence does not end in an infinite string of 0's.
Definition
We define a map
 (0,1)
as follows:
(0,1)
as follows:
Given
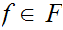 ,let
d(i)=.d
,let
d(i)=.d d
d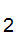 d
d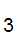 ......d
......d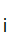 , the ith. (finite) partial fraction.
, the ith. (finite) partial fraction.
Let
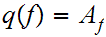
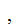 where,
where,
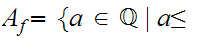 d(i)
for
some i
d(i)
for
some i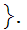
9.6 Lemma:
 (0,1)
is one to one and onto, hence
(0,1)
is one to one and onto, hence
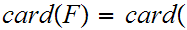 (0,1)
(0,1)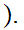
Proof:
As before, but note that in the definition of
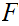 ,
had we not excluded .99999999...,
,
had we not excluded .99999999...,
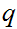 would have produced
would have produced
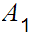

In the text, the notation
"c" is used
for 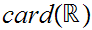 .
In these notes we will stick to the second notation.
.
In these notes we will stick to the second notation.
The proof of the following theorem turns out to be deceptively straight forward, given the material that we will discuss on Page 14.
9.7 Theorem:

Proof:
Using 9.5 and 9.6, it suffices
to show,
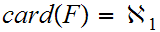 , which in turn ,applying 9.1, requires producing 1 to
1 maps
, which in turn ,applying 9.1, requires producing 1 to
1 maps
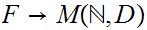 and
and
 .
.
One direction is trivial since inclusion gives a one to one into map

Next let
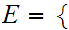 1,2,3,4,5,6,7,8
1,2,3,4,5,6,7,8
Apply 9.5 to conclude that
 ,
hence there is a 1 to 1 onto map
,
hence there is a 1 to 1 onto map
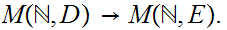 Finally,
composing this with the inclusion
Finally,
composing this with the inclusion
 gives a 1 to 1 map
gives a 1 to 1 map
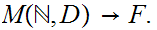
From the point of view of set maps we have natural strict inclusions.
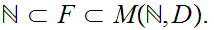 We have to make a choice for
We have to make a choice for
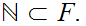 We have shown
We have shown
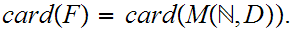
It is not difficult to find other sets between
 and
and
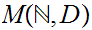 of size
of size
 The natural question to ask is are other cardinalities between
The natural question to ask is are other cardinalities between
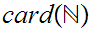 and
and
 ?
In particular, can we find a set
?
In particular, can we find a set
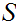 such that
such that

and
 ?
?
Cantor conjectured that this was not possible. We shall see that this conjecture has has resulted in some very interesting mathematics.
Evidence - Measure
Working Definition - Let
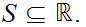 We say that has measure 0, if for any
We say that has measure 0, if for any
 there exists a, possibly countable, set of closed intervals
there exists a, possibly countable, set of closed intervals
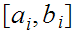 of length greater than 0 such that
of length greater than 0 such that
 and
and 
1 . If
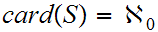 then
then 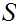 has measure 0.
has measure 0.
choose some 1 to 1, onto map
 .
For each
.
For each
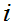 choose
choose
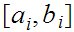 such that
such that
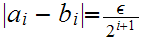 and
and
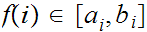
note that
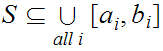 and
and 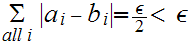
For example if
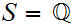 , and
, and
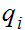 is the
i
is the
i rational
in some ordering of the rationals by
rational
in some ordering of the rationals by
 then set
then set

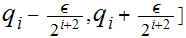
2. The Cantor Middle Third Set -
Take the closed unit interval [0,1] and delete the open middle third (1,3)
Call the resulting set
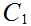 . note that the "length" of
. note that the "length" of
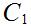 , equal the sum of the lengths of the intervals in
, equal the sum of the lengths of the intervals in
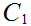 ,
is
,
is
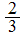
Suppose we have defined
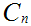 as a union of closed intervals in [0,1], and that the length of
as a union of closed intervals in [0,1], and that the length of
 is
is
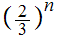 .
.
Define
 to be the result of deleting the open middle third out of each of the
intervals in
to be the result of deleting the open middle third out of each of the
intervals in
 .
.
Note that the length of
 is
is
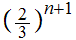
Finally, define
 Almost by definition,
Almost by definition,
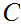 has measure 0. On the other hand
has measure 0. On the other hand
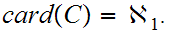
Check that
 is more or less,
is more or less,
 0,2
0,2 ,using base three arithmetic.
,using base three arithmetic.