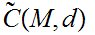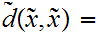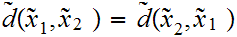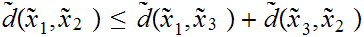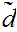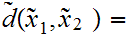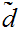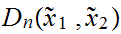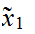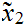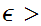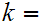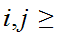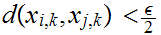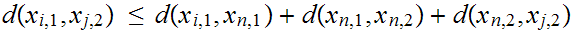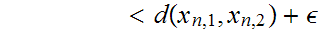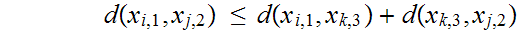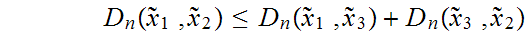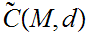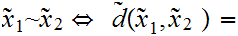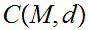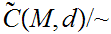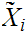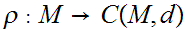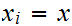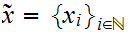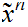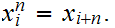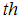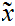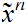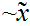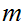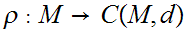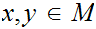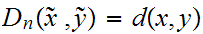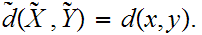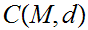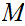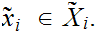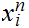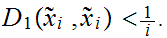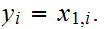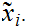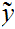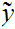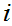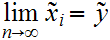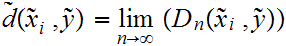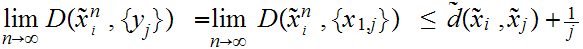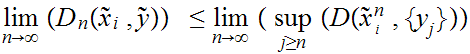22. Every
Metric Space can be Isometrically Embedded in a Complete Metric Space - I
We offer two proofs that every Metric Space can be Isometrically Embedded in
a Complete Metric Space. The first has the virtue of being modeled on the
usual proof using Cauchy sequences. It's downside is in its complexity since
the members of the Completion are equivalence classes of Cauchy sequences.
22.1
Definitions, Remarks, Observations, and Notation:
-
We will use the notation
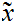 as short hand for
as short hand for
 .
We will also use the notation
.
We will also use the notation
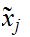 for
indexed sets of sequences
for
indexed sets of sequences
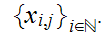
-
Given a Metric Space
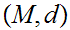 and subsets
and subsets
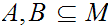 , we define
, we define
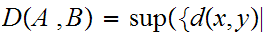
 and
and

In general
 takes
values in
takes
values in

-
Given sequences
 1
1 and
and
 it will be convenient to define
it will be convenient to define
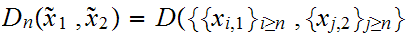
-
Finally we define
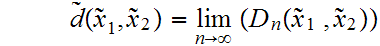
Note that if
 is finite for any n ,then
is finite for any n ,then
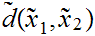 is finite since
is finite since
0

-
Note that, almost by definition, a sequence
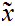 is
a Cauchy sequence if and only if
is
a Cauchy sequence if and only if
 0.
0.
-
Given a Metric Space
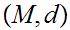 we let
we let
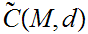 denote
its Set of Cauchy Sequences.
denote
its Set of Cauchy Sequences.
--------------------------------------------------------------------------------------------
22.2 Theorem:
 is
well defined on the Set
is
well defined on the Set
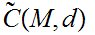 ,and
satisfies the following metric properties :
,and
satisfies the following metric properties :
-
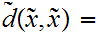 0
0
-
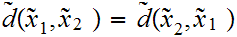
-
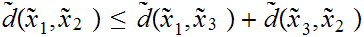
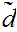 is
called a psudo-metric since one can have
is
called a psudo-metric since one can have
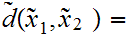 0
but
0
but

Proof:
To show that
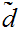 is
well defined. It suffices to show that
is
well defined. It suffices to show that
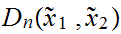 is bounded for some n. Since
is bounded for some n. Since
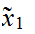 and
and
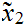 are Cauchy,
are Cauchy,
choose
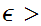 0
, and n such that for
0
, and n such that for
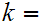 1
or 2 and
1
or 2 and
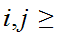 n
n
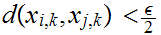
thus,
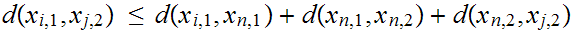
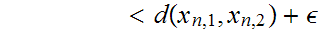
2. is
immediate. To prove 3. observer that, in general,
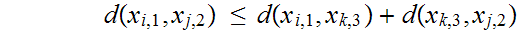
hence
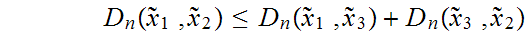
------------------------------------------------------------------------
22.3 Definitions, Observations, and Notation:
-
Based on 22.2, we can define an equivalence relation
on
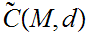 by setting
by setting
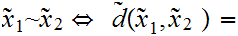 0.
We use the notation
0.
We use the notation
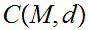 for
for
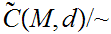 .
.
-
One checks that
 induces
a metric on
induces
a metric on
 . We use the same notation for this induced metric. On the other hand, we will
use
. We use the same notation for this induced metric. On the other hand, we will
use
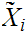 to
denote the equivalence class of Cauchy sequences containing
to
denote the equivalence class of Cauchy sequences containing
 .
.
-
Define a Set map
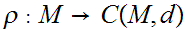 by the formula
by the formula

 ,
the equivalence class of
,
the equivalence class of
 ,where
,where
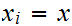 for all
for all

We will want the following
calculation.
22.4
Lemma:
Given a Cauchy sequence
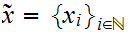 ,for
each n can can define a sequence
,for
each n can can define a sequence
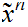 where
where
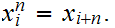 This
is called the
n
This
is called the
n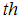 tail of
tail of
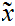 . Then
. Then
-
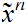 is Cauchy
is Cauchy
-

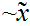 .
.
Proof:
Easy, To Be Turned in (Due Wed. April
20)
----------------------------------------------------------------------
Solution:
For any
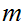 ,
, so
so

As well as,
 .
.
Thus
 0
0
---------------------------------------------------------------------------
22.5 Theorem:
 is
a Complete Metric Space. Moreover,
is
a Complete Metric Space. Moreover,
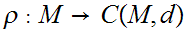 is a dense isometric embedding.
is a dense isometric embedding.
Proof:
To verify that
 is
an isometric embedding note that for any n and
is
an isometric embedding note that for any n and
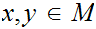
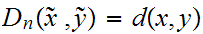 and thus
and thus
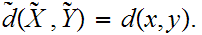
That the embedding is dense, is the usual argument that a Cauchy sequence is
the limit of its terms.
Next, given a Cauchy sequence
 in
in
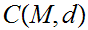 we define a sequence
we define a sequence
 in
in
 as follows:
as follows:
One next verfies that
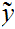 is Cauchy and
is Cauchy and

That
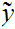 is Cauchy follows from the observation that, in general
is Cauchy follows from the observation that, in general


For any n.
In the limit

which goes to 0 as
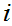 and
and
 .
.
To show that
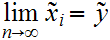 is a similar argument
is a similar argument
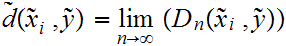
Also
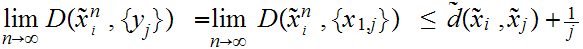
But
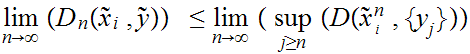
which goes to
0 as
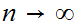
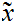 as short hand for
as short hand for
 .
We will also use the notation
.
We will also use the notation
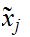 for
indexed sets of sequences
for
indexed sets of sequences
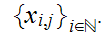
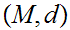 and subsets
and subsets
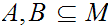 , we define
, we define
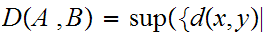
 and
and

 takes
values in
takes
values in

 1
1 and
and
 it will be convenient to define
it will be convenient to define
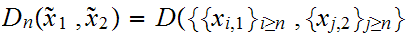
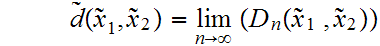
 is finite for any n ,then
is finite for any n ,then
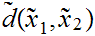 is finite since
is finite since

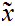 is
a Cauchy sequence if and only if
is
a Cauchy sequence if and only if
 0.
0.
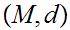 we let
we let
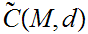 denote
its Set of Cauchy Sequences.
denote
its Set of Cauchy Sequences.