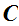 consists
of:
consists
of:
16.1 Definition:
A category
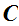 consists
of:
consists
of:
a class of objects, written
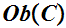
For every two objects
 and
and
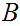 in
in
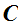 ,
a set
,
a set
 of morphisms from
of morphisms from
 to
to
 such that if
such that if
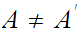 and/or
and/or
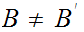 then
then
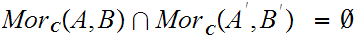 .
One writes
.
One writes
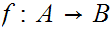 or
or
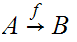 for
for 
For every three objects
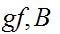 and
and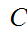 ,
there is a binary operation
,
there is a binary operation
 called composition (we write
called composition (we write
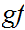 or
sometimes
or
sometimes  )such
that the following axioms hold:
)such
that the following axioms hold:
a. associativity:
If
 ,
,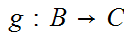 ,
and
,
and
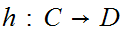 then
then
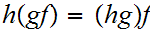 ,
,
b. identity:
For every object
 there exists a morphism
there exists a morphism
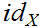
 called
the identity morphism for
called
the identity morphism for
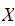 ,
such that for every morphism
,
such that for every morphism
 we have
we have
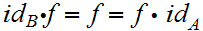 .
.
16.2 Examples:
The Category of Sets -
The Categories of posets, Ordered, or Well Ordered Sets -
The Category of Metric Spaces -
The Category or Groups, Rings, Fields etc -
16.3 Theorem:
In any Category
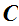 the
identity morphisms are unique.
the
identity morphisms are unique.
Proof:
Suppose we have and object
 and two morphisms
and two morphisms
 and
and
 that
both
that
both
satify 16.1 b. Then
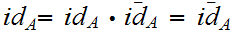 .
.
16.4 Definition:
Fixing a Category,
A morphism
 is
called an epimorphism if for any object
is
called an epimorphism if for any object
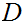 and
morphisms
and
morphisms
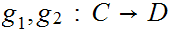 ,
,
 if
and only if
if
and only if
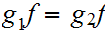
A morphism
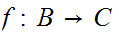 is
called a monomorphism if for any object
is
called a monomorphism if for any object
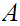 and
morphisms
and
morphisms
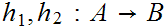 ,
,
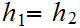 if
and only if
if
and only if
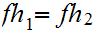 .
.
16.5 Examples:
The Category of Sets - onto is equivalent to epimorphism, and one to one is equivalent to monomorphism.
The Category of Metric Spaces - Consider
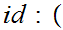 0,1
0,1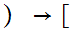 0,1
0,1![$\QTR{Large}{]}$](graphics/categorytheory__47.png) . This is an epimorphism.
. This is an epimorphism.
Exercise Prove this. ( Hint- Review the definition of continuity)
One can find examples of monomorphisms that are not one to one as Set maps.