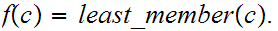and
and
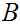 ,
either
,
either
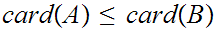 or
or
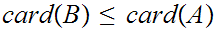 . In particular, we need to show that there exists a 1 to 1 map
. In particular, we need to show that there exists a 1 to 1 map
Discussion:
Our goal in this section is to show that for any two sets
 and
and
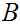 ,
either
,
either
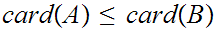 or
or
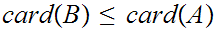 . In particular, we need to show that there exists a 1 to 1 map
. In particular, we need to show that there exists a 1 to 1 map
 or a 1 to 1 map
or a 1 to 1 map
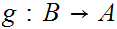 .
(or both).
.
(or both).
In order to meet our goal we have to augment the Zermelo-Frankel axioms.
10. 1 Axiom:(Zorn's Lemma) Let
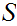 be
a poset under
be
a poset under
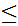 . Suppose every chain in
. Suppose every chain in
 has
an upper bound, then
has
an upper bound, then
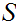 has a maximal element. That is, there exists an element
has a maximal element. That is, there exists an element
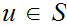 such that for no
such that for no
 is it the case that
is it the case that
 .
.
For Discussion:
Consider well ordering vs. Zorn's Lemma as they apply to
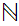 .
.
Consider well ordering vs. Zorn's Lemma as they apply to
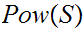 , any
, any
Look at Tarski's Theorem and compare it to Zorn's Lemma
10. 2 Theorem:
For any two sets
 and
and
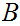 ,
either there exists a 1 to 1 map
,
either there exists a 1 to 1 map
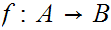 or a 1 to 1 map
or a 1 to 1 map
 .
(or both).
.
(or both).
Proof:
Define a poset
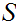 whose elements are all pairs
whose elements are all pairs
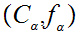 with
with
 and with
and with
 one to one
one to one
We set
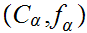

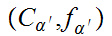 if
if
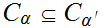 and
and
 .
Clearly
.
Clearly
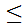 is a partial ordering.
is a partial ordering.
Moreover, any chain
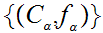 has a least upper bound, in particular, the pair
has a least upper bound, in particular, the pair
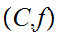 given
by
given
by
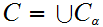 and
and
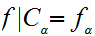 .
.
Therefore, by Zorn's Lemma there exists a maximal element
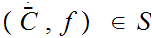 .
Either
.
Either
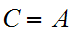 or
or
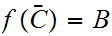 if not we could choose
if not we could choose
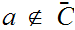 and
and
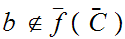 and define
and define
the pair
 where
where
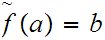 and
and
 .
Contradicting the maximality of
.
Contradicting the maximality of
 .
.
We now prove the following,
10.3 Theorem:
In the presence of Zorn's Lemma every Set can be Well Ordered.
Proof:
Given a Set
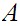 ,
Define a poset
,
Define a poset
 whose elements are all pairs
whose elements are all pairs
 with
with
 and
and
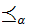 a Well Ordering of
a Well Ordering of
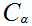 . We now copy the previous proof, replacing
. We now copy the previous proof, replacing
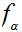 with
with
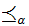 appropriately. Care has to be taken with the definition of
appropriately. Care has to be taken with the definition of
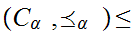
 because we will need to know that the lub
because we will need to know that the lub
 inherits a Well Order from the
inherits a Well Order from the
 .
.
We define
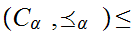
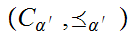 by
the following three properties.
by
the following three properties.
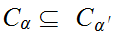
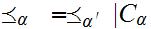
If
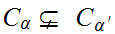 then
then
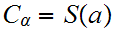 for some
for some
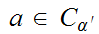 .
.
Now let
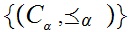 be a chain. As above, we verify that the pair
be a chain. As above, we verify that the pair
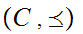 is
a lub, where
is
a lub, where
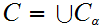 and
and
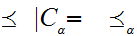 . The one thing that requires some proof is that
. The one thing that requires some proof is that
 is Well Ordered.
is Well Ordered.
Let
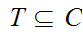 be a none empty Set. One needs to show that
be a none empty Set. One needs to show that
 has a least member. Pick any
has a least member. Pick any
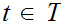 .
.

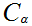 for
some
for
some
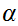 . Let
. Let
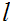 be
the least member of
be
the least member of

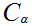 .
.
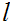 is also the least member
is also the least member
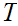 because if
because if
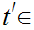
 and
and

 ,
then
,
then
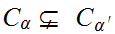 and
thus, by 3.,
and
thus, by 3.,

Finally, invoking Zorn's Lemma, choose a maximal Well Ordered subset
 .
.
Again,
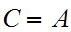 .
If not, again as before chose
.
If not, again as before chose
 and
and 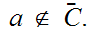
Define a Well Order on
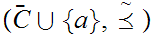 by setting
by setting
 for
for
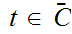 and letting
and letting
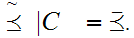
10.4 Axiom:
The Well Ordering Principle states that every Set can be Well Ordered.
10.5 A restatement of 10.3:
Zorn's Lemma implies the Well Ordering Principle.
We close this Page by stating
10.6 The Axiom 0f Choice:
Let
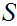 be a set and
be a set and
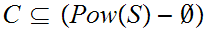 . There exists at least one map
. There exists at least one map
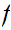
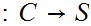 ,
,
such that
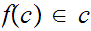
 for
each set
for
each set
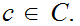
and proving
10.6 Theorem:
The Well Ordering Principle implies the Axiom of Choice.
Proof:
Choose a Well Ordering of
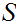 .
Introducing some obvious notation, let
.
Introducing some obvious notation, let