 is said to be partially ordered or a poset
if there is a binary relation
"
is said to be partially ordered or a poset
if there is a binary relation
"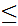 "
defined on
"
defined on
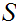 satisfying the following three properties
satisfying the following three properties
Assignment: Study the material in 1.2 of the text.
6.1 Definition:
A Set,
 is said to be partially ordered or a poset
if there is a binary relation
"
is said to be partially ordered or a poset
if there is a binary relation
"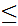 "
defined on
"
defined on
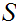 satisfying the following three properties
satisfying the following three properties
For all

For all
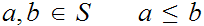 and
and
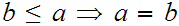
For all
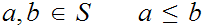 and
and

 It is (totally)ordered if it also
satifies
It is (totally)ordered if it also
satifies
For all
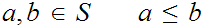 or
or
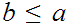
6.2 Definition:
Given a partially ordered set
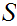 ,
we call
,
we call
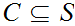 a chain of
a chain of
 if it is totally ordered.
if it is totally ordered.
6.3 Lemma:
Let
 . It is a simple matter to check that any a partial/total order on
. It is a simple matter to check that any a partial/total order on
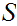 ,
restricts to a partial/total order on
,
restricts to a partial/total order on
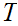 .
.
Proof: Verify for yourself.
6.4 Definition:
Given partially ordered sets
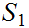 and
and
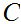 , a one to one onto map
, a one to one onto map
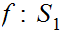
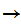
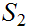 is called an order isomorphism if
is called an order isomorphism if
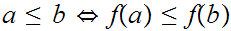 for all
for all
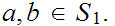
6.4.1 Lemma:Let
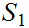 be ordered and
be ordered and
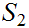 be a poset. Suppose we are given a one to one onto map
be a poset. Suppose we are given a one to one onto map
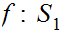
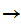
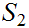 such that
such that
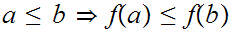 for all
for all
 then:
then:
1.
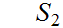 is ordered
is ordered
2.
 is an order isomorphism.
is an order isomorphism.
3.If
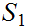 is Well Ordered so is
is Well Ordered so is

Proof:
1. Let
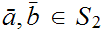 and
and
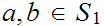 be such that
be such that
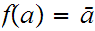 and
and

Since
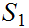 is ordered
is ordered
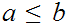 or
or
 and thus
and thus
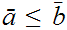 or
or
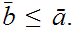
2. We need only show that for all
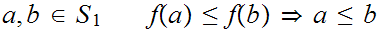 . Since
. Since
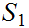 is ordered
is ordered
 or
or

But
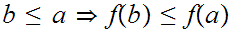 and by hypothesis
and by hypothesis
 so
so
 and,
and,
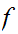 since
is one to one,
since
is one to one,
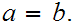
Thus we have

3. Let
 . Since
. Since
 is Well Ordered let
is Well Ordered let
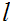 be the least element of
be the least element of
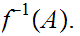
Check that
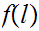 is the least element of
is the least element of
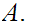
Examples:
 and
and
 are
all ordered by the usual binary relations.
are
all ordered by the usual binary relations.
Let
 . Let
. Let
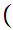 m,n
m,n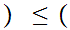 r,s
r,s iff
m
iff
m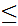 r
and
n
r
and
n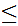 s.
This is partial ordering but not a total ordering. Compare
s.
This is partial ordering but not a total ordering. Compare
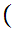 1,2
1,2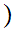 and
and
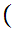 2,1
2,1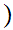
Let
 be the subset
be the subset
 1,n
1,n all n.
all n.
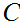 is
a chain.
is
a chain.
Let
 and
and
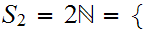 2,4,6,....,2n...
2,4,6,....,2n...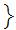 then
then
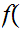 n
n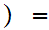 2n
is an order isomorphism.
2n
is an order isomorphism.
6.5 Definition:
Let
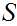 be Ordered. Let
be Ordered. Let
 Define,
Define,
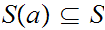 , called the segment defined by
, called the segment defined by
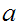 as follows.
as follows.
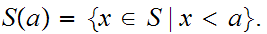
If
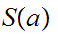 is
finite it will be convenient to use the notation
is
finite it will be convenient to use the notation
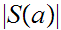 for
the number of member in
for
the number of member in
 .
.
Example: In
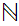 with the usual ordering
with the usual ordering
 n
n and
and
 n
n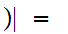 n-1.
n-1.
6.6 Definition: A Set,
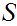 is said to be Well Ordered (WO) if it is Ordered and every
subset
is said to be Well Ordered (WO) if it is Ordered and every
subset
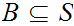 has a least member. That is there exists an
has a least member. That is there exists an
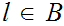 such that for all
such that for all
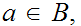
 .
Note that by 6.1.2. above, we know that
.
Note that by 6.1.2. above, we know that
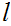 is unique.
is unique.
It is enough to assume that
 is partially ordered and every subset has a least element?
is partially ordered and every subset has a least element?
Any subset of a Well Ordered Set is Well Ordered, using the same order.Why?
Examples:
Any Ordering of a finite set is a Well Ordering.
Assignment: Due Feb. 9: Show that any two orderings of a given finite set are order isomorphic.
 is Well Ordered by the usual binary relation. Absent any qualifications, when
we use the symbol
is Well Ordered by the usual binary relation. Absent any qualifications, when
we use the symbol
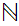 this is the order that is implied.
this is the order that is implied.
Let
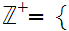 0,1,2,3,4,5,..n,...
0,1,2,3,4,5,..n,... with the usual order. Then
with the usual order. Then
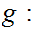
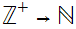 defined by the
defined by the
formula  x
x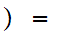
x
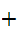 1
is an order isomorphism.This is what we "mean" when we say the Natural Numbers
can be defined either as
1
is an order isomorphism.This is what we "mean" when we say the Natural Numbers
can be defined either as
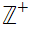 or
or
 .
.
 and
and
 are
not Well Ordered by the usual binary relation.
are
not Well Ordered by the usual binary relation.
6.7 Theorem:
Suppose that we have a proposition
 n
n .
.
Suppose
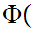 1
1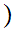 is true
is true
and
for all
n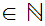 ,
,
 n
n n
n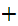 1
1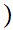 is true .
is true .
Then,
for all
n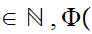 n
n is true .
is true .
Proof:
Let
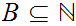 be the set of all n for which
be the set of all n for which
 n
n is not true. Suppose
is not true. Suppose
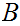 were not empty. Then it has a least element, l . Since
were not empty. Then it has a least element, l . Since
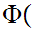 1
1 is true, l
is true, l
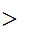 1.
We know that
1.
We know that
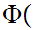 l
l
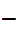 1
1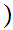 is true. But
is true. But
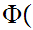 l
l
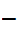 1
1 l
l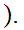 Therefore
Therefore
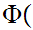 l
l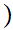 is
true. Hence
is
true. Hence
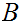 is empty.
is empty.
6.8 Theorem:
a. Given
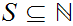 , for any
, for any
 ,
,
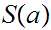 is
finite.
is
finite.
Moreover,
b. either
 is
finite or for any integer n
is
finite or for any integer n
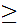 0
we can find a unique
0
we can find a unique
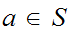 with
with
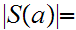 n.
n.
Hence.
c. There exists an order isomorphism
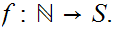
Proof:
a. Is immediate from the observation that since
 ,
,
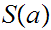 is a subset of the segment of
is a subset of the segment of
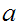 in
in
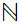 ,
which is finite.
,
which is finite.
b. Is a simple induction argument. Let
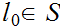 to be the least element of
to be the least element of
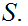
Since
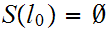 we have
we have
 0
. Moreover uniqueness follows from the fact that
0
. Moreover uniqueness follows from the fact that
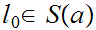 for any
for any
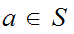 and
and
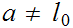
Hence
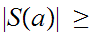 1.
1.
Assume that for 0
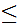 i
i
 n
we can find a unique
n
we can find a unique
 with
with
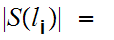 i.
i.
Since by assumption
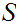 is
not finite, let
is
not finite, let
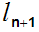 be the least element of
be the least element of

We need to verify that

 ,
,
hence
 n+1.
n+1.
First note that
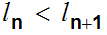 ,
since if
,
since if
 then
then
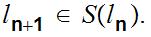
So
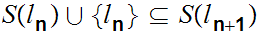
On the other hand if
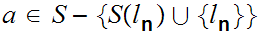
and
 then
then
 .
thus
.
thus
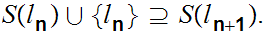
Again uniqueness follow from the fact that since
 for any
for any
 and
and
 we
conclude that
we
conclude that

we can now apply the principal of mathematical induction.
c. follows from b.
First define
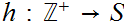 by the formula
by the formula
 n
n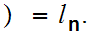
Clearly
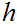 is one to one. If it were not onto let
is one to one. If it were not onto let
 and
and

Suppose
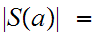 m.
Then
m.
Then
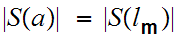 contradicting the uniqueness of
contradicting the uniqueness of
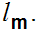
Finally, let
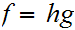 where
where
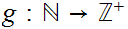 is defined by the formula
is defined by the formula
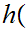 n
n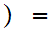 n-1
n-1
6.9 Theorem:
Let
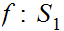
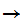
 be an order isomorphism. . Then
be an order isomorphism. . Then
1. for all
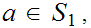
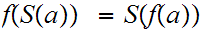
2. if
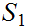 (or
(or
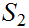 )
is Well Ordered
)
is Well Ordered
so is
 (or
(or
 )
)
Assignment: Due Feb. 9: Prove this
Solution: See 6.4.1 above.
Example:
Let
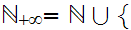
 where
where
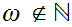 .Define
an ordering
.Define
an ordering
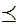 on the
on the
 as follows:
as follows:
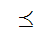
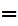
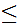 ,the usual ordering, on
,the usual ordering, on
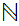 and for all
n
and for all
n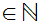 we
have
we
have
 n
n

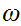 .
.
Assignment: Due Feb. 9: Show that
1. There exist a one to one onto set
map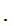
2.
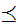 is a Well Ordering
is a Well Ordering
3.
 is not order isomorphic to
is not order isomorphic to
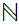 with the usual ordering.
with the usual ordering.
(Hint:) Use 6.8 and 6.9 to prove 3.
Solution: We give the details for 3.
Let
 be an order isomorphism. Suppose
be an order isomorphism. Suppose
 n
n By 6.9.3
By 6.9.3
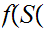 n
n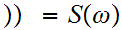 ,which is not possible since
,which is not possible since
 n
n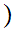 contains a finite number of elements and
contains a finite number of elements and
 does
not.
does
not.
Finally, we gather results above to state the following theorem, which characterizes Set Theory for the Natural Numbers.
6.10 Theorem:
For any
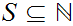
1. There exists an n and an order isomorphism
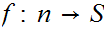
or
2. There exists an order isomorphism
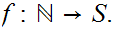
Examples:
While
 the set of fractions greater than 0, is not well ordered by the usual
ordering, it is not hard to put a non-standard well ordering on
the set of fractions greater than 0, is not well ordered by the usual
ordering, it is not hard to put a non-standard well ordering on
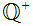 .
.
Referring back to Page 0, consider the function
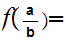 2
2 3
3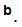 Check
that this is 1 to 1, hence
Check
that this is 1 to 1, hence
 inherits a well ordering from
inherits a well ordering from
 .
This is certainly not the usual ordering since
.
This is certainly not the usual ordering since
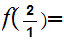 12
and
12
and
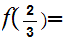 108.
hence
2
108.
hence
2 (
(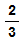 ).
Note as well that
).
Note as well that
 inherits a form of mathematical induction from this well ordering albeit not a
particularly useful one.
inherits a form of mathematical induction from this well ordering albeit not a
particularly useful one.