13.The Axiom of Choice


Eric Schecter's "Axiom of Choice Home Page"

On this Page we complete the cycle of equivalences started on Page 10 by showing that the Axiom of Choice implies Zorn's Lemma.

The Axiom of Choice

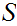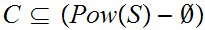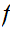
Let $\QTR{Large}{S}$ be a set and MATH . There exists at least one function $\QTR{Large}{f}$ MATH ,

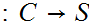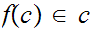
such that MATH $\ $for each set MATH

 

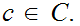
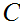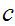Less formally, Let $\QTR{Large}{C}$ be a set of non empty sets, there exist choice functions, which allows us to select a member of $\QTR{Large}{c}$ for each MATH.

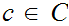In postulating the existence of this functions one is in no way claiming that they arose from some given, known, rule. The choice functions are the rules and we can use them without knowing anything about them!

 

Zorn's Lemma

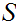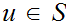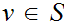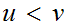Let $\QTR{Large}{S}$ be a poset under $\QTR{Large}{\leq }$ . Suppose every chain in $\QTR{Large}{S}$ has an upper bound, then $\QTR{Large}{S}$ has a maximal element. That is, there exists an element MATH such that for no MATH is it the case that $\QTR{Large}{u<v}$.

 

The Well Ordering Principle

Every set can be well ordered.

 

13. 1 Theorem

  1. Zorn's Lemma implies The Well Ordering Principle.

  2. The Well Ordering Principle implies The Axiom of Choice

  3. The Axiom of Choice implies Zorn's Lemma

Proof:

1. and 2. were proved on Page 10. We now show 3.

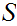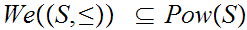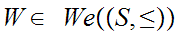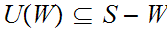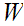Suppose we are given a poset MATH $\QTR{Large}{)}$. Suppose it satifies the hypothesis of Zorn's Lemma. That is, every chain in $\QTR{Large}{S}$ has an upper bound. Again, let MATH bet the Well Ordered subsets. Finally, for MATH, let MATH be the set of upper bounds of $\QTR{Large}{W}$ (excluding, possibly, the top element, if it exists). If Zorn's Lemma is false for

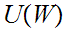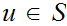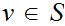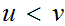MATH $\QTR{Large}{)}$, $\QTR{Large}{U(W)}$ is never empty, because for any MATH there is a MATH such that $\QTR{Large}{u<v}$.

Applying the Axiom of Choice to 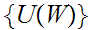MATH , select any

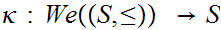MATH such that MATH

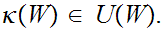
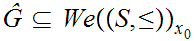Next choose MATH and let MATH be defined by the property that 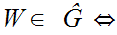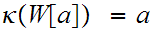MATH (MATH for all MATH . Clearly MATHis not empty, it contains MATH ,and it satisfies the hypotheses of 12.7.

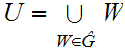
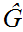So MATH MATH. But MATH is defined on all of MATHso, we could augment $\QTR{Large}{U}$ with MATH which must also belong to MATH contradicting the definition of $\QTR{Large}{U}$.