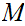17. Some Interesting Subsets of the Plane

17.1 Definition:

For the moment we will focus on the plane and some of its subsets. Abstracting the notion of Euclidian distance,

A Metric Space is a set 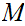$\QTR{Large}{M}$ and a function MATH. We write MATH

such that for all MATHin $\QTR{Large}{M}$:

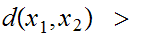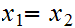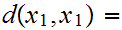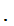
  1. Positivity: MATH0 unless MATH in which case MATH0$\QTR{Large}{.}$

  2. Symmetry: For all MATH

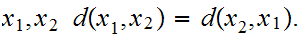
  3. Triangle Inequality: For all MATH

17.1.4 Lemma:

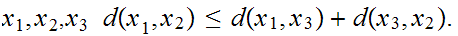
The the Triangle Inequality has a second, equivalent form:

For all MATH

*MATH

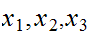
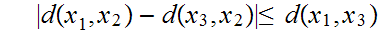
Proof:

Note that both formulas are symetric in MATH and MATH thus we may assume that

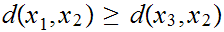MATH . Thus * can be written

$\qquad \qquad $0 MATH

That this is equivalent to 17.1.3 is a matter of adding or subtracting equals from both sides of the two inequalities.

17.2 Interesting Subsets of the Plane:

The first collection of examples are the various "real lines". The x-axis - the y-axis - other subsets of the form.

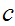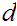$\QTR{Large}{cx+dy}$ where $\QTR{Large}{c}$ and $\QTR{Large}{d}$ are constants. Euclidian distance is really the only metric that comes to mind for these examples. That is,

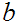if $\QTR{Large}{a}$ and $\QTR{Large}{b}$ are two points on a line then MATH

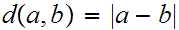
Once we step away from lines, the importance of abstracting the definition of metric becomes a bit clearer. Consider the circle

MATH

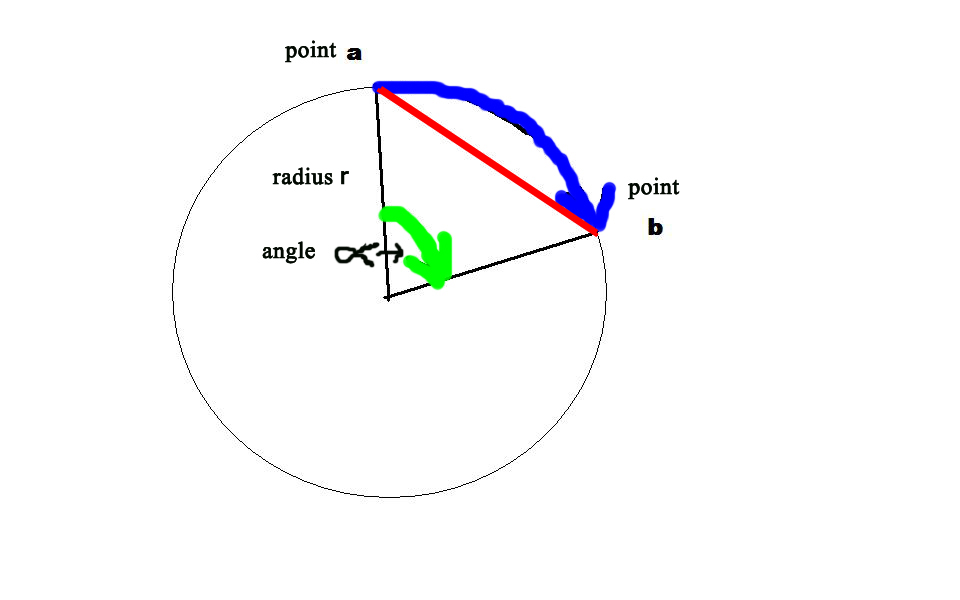
There are three metrics illustrated in the diagram.

  1. MATH

  2. MATH

  3. MATH

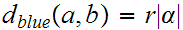
The question to be considered is what is the relationship between the three. Functionally, of course,

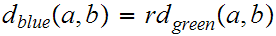
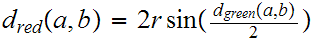
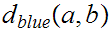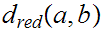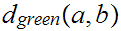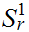Which seems to say that MATH and MATH are somehow related, but MATH may not be. In point of fact, these three metric generate the same "Topology" on MATH , read for the moment "define the same set of continuous function. On the next Page we make this precise.