 and a function
and a function
 .
We write
.
We write
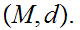
For the moment we will focus on the plane and some of its subsets. Abstracting the notion of Euclidian distance,
A Metric Space is a set
 and a function
and a function
 .
We write
.
We write
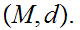
such that for all
 in
in
 :
:
Positivity:
 0
unless
0
unless
 in which case
in which case
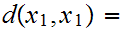 0
0
Symmetry: For all
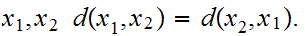
Triangle Inequality: For all
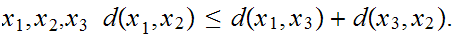
The the Triangle Inequality has a second, equivalent form:
For all
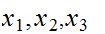
*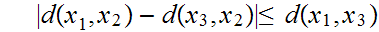
Fix a Metric Space
 and a point
and a point
Given
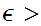 0
we define the open ball of radius
0
we define the open ball of radius
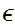 around
around
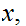


We say
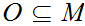 is open if for any
is open if for any
 there exist an
there exist an
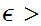 0
such that
0
such that
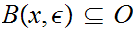
The set of open sets is called the Topology defined by the Metric.
In a Metric Space

 and
and
 (the empty set) is open
(the empty set) is open
Let
 be an arbitrary set of open sets, then
be an arbitrary set of open sets, then
 is
also open.
is
also open.
Let
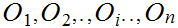 be
a finite set of open sets, then
be
a finite set of open sets, then
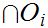 is
also open.
is
also open.
Given Metric Spaces
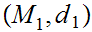 ,
,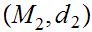 and a function
and a function
 .
We say that
.
We say that
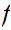 is continuous a point
is continuous a point
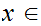
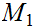 if given any
if given any
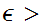 0
there is a
0
there is a
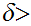 0
such that
0
such that
 .
.
We say that
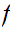 is continuous if it is continuous at every point.
is continuous if it is continuous at every point.
Given Metric Spaces
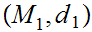 ,
,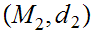 ,a function
,a function
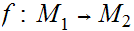 is continuous if and only for every open set
is continuous if and only for every open set

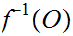 is open in
is open in
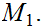
19.1 Definition:
Let
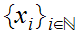 be a sequence in a Metric Space
be a sequence in a Metric Space
 .
We say the sequence converges to
.
We say the sequence converges to
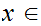
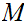 ,
written
,
written
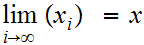 ,
if for any
,
if for any
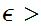 0 there
exists an
n
0 there
exists an
n such that
such that
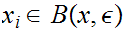 for
n
for
n .
.
19.2 Theorem:
Given Metric Spaces
 ,
, and a function
and a function
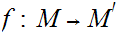 ,
,
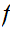 is continuous a point
is continuous a point
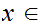
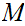 if and only if for every
if and only if for every
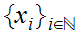 ,
,
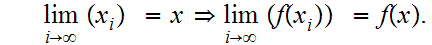 Note that this implies that
Note that this implies that
 is is continuous at every point if and only if for every convergent sequence
is is continuous at every point if and only if for every convergent sequence

19.3 Definition:
Given a Metric Space
 ,
and a subset
,
and a subset
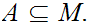 Define
Define
 and
and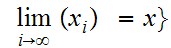
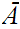 is called the closure of
is called the closure of
 .
.
19.4 Lemma:
 For
any
For
any
 ,
,
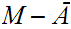 is open.
is open.
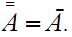 That is, the closure of the closure of
That is, the closure of the closure of
 is
the closure of
is
the closure of
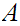 .
.
19.5 Definition:
We call a subset
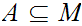 dense if
dense if
 .
.
Example:
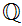 is dense in
is dense in
 .
.
20.1 Definition:
A sequence
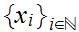 in a Metric Space
in a Metric Space
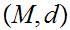 is called a Cauchy Sequence
is called a Cauchy Sequence
if for any
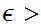 0 there
exists an
n
0 there
exists an
n such that if
such that if
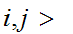 n
n then
then
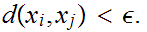
20.2 Lemma:
In the setting of 20.1 , every Cauchy sequence is
bounded. In particular there is a number
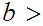 0
and
an
0
and
an  such that
such that

20.5 Definition:
A Metric Space is called complete if every Cauchy sequence converges. In particular,
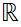 is a complete metric space.
is a complete metric space.
20.8 Definition:
Given Metric Spaces
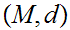 and
and
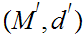 and a map
and a map
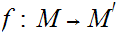 we say that
we say that
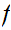 is
is
uniformly continuous if for all
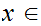
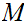 ,given any
,given any
 0
there is a
0
there is a
 0
such
that
0
such
that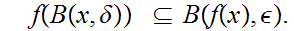 Note
that this differs for continuity in that
Note
that this differs for continuity in that
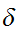 is
independent of
is
independent of
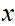 .
.
21.1 Definition:
Given a Metric Space
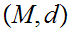 ,
and a subset
,
and a subset
 we
say
we
say
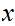 is
a limit point of
is
a limit point of
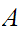 if
if
____________
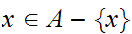 .
.
That is
 is
in the closure of
is
in the closure of
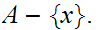
Note:
It is not necessarily the case that the set of limit points of
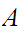 is
the closure of
is
the closure of
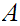 .
.
For
example, a singleton set
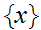 has no limit points but is its own closure.
has no limit points but is its own closure.
21.2 Definition:
A Metric Space,
 ,
is called compact if every infinite subset
,
is called compact if every infinite subset
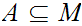 has
a limit point.
has
a limit point.
21.4 Theorem:
Let
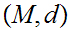 be
a Metric Space. The following are equivalent:
be
a Metric Space. The following are equivalent:
 is
compact.
is
compact.
Every sequence in
 has a convergent subsequence.
has a convergent subsequence.
21.4.1 Corollary:
Every compact Metric Space is complete:
21.5 Theorem:
Given a compact Metric Spaces
 :
:
For any
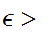 0
and some
n
0
and some
n there exists points
there exists points
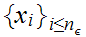
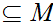
such that
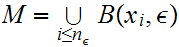 .
.
In particular, M is bounded in the sense that there exists some
b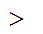 0
such that
0
such that
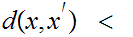 b for
any
b for
any
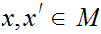 .
.
21.6 Theorem:
Every compact metric space has a countable dense subset.
21.7 Theorem:
Given Metric Spaces
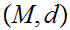 and
and
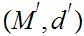 with
with
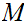 compact, and a continuous map
compact, and a continuous map
 then
then
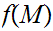 is compact.
is compact.
21.8 Theorem:
Given Metric Spaces
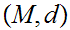 and
and
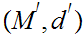 with
with
 compact, and a continuous map
compact, and a continuous map
 then
then
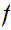 is also uniformly continuous.
is also uniformly continuous.
We will use the notation
 as short hand for
as short hand for
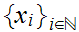 .
We will also use the notation
.
We will also use the notation
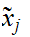 for
indexed sets of sequences
for
indexed sets of sequences
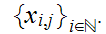
Given a Metric Space
 and subsets
and subsets
 , we define
, we define
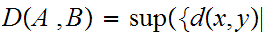
 and
and

In general
 takes
values in
takes
values in
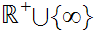
Given sequences
 1
1 and
and
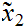 it will be convenient to define
it will be convenient to define
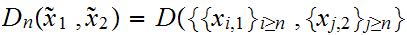
Finally we define

Note that if
 is finite for any n ,then
is finite for any n ,then
 is finite since
is finite since
0
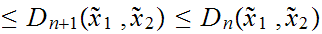
Note that, almost by definition, a sequence
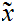 is
a Cauchy sequence if and only if
is
a Cauchy sequence if and only if
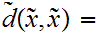 0.
0.
Given a Metric Space
 we let
we let
 denote
its Set of Cauchy Sequences.
denote
its Set of Cauchy Sequences.
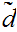 is
well defined on the Set
is
well defined on the Set
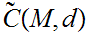 ,and
satisfies the following metric properties :
,and
satisfies the following metric properties :
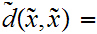 0
0
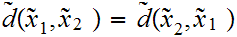
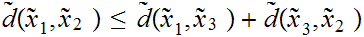
Based on 22.2, we can define an equivalence relation
on
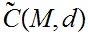 by setting
by setting
 0.
We use the notation
0.
We use the notation
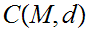 for
for
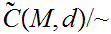 .
.
One checks that
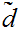 induces
a metric on
induces
a metric on
 . We use the same notation for this induced metric. On the other hend, we will
use
. We use the same notation for this induced metric. On the other hend, we will
use
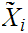 to
denote the equivalence class of Cauchy sequences containing
to
denote the equivalence class of Cauchy sequences containing
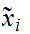 .
.
Define a Set map
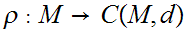 by the formula
by the formula
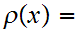
 ,
the equivalence class of
,
the equivalence class of
 ,where
,where
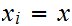 for all
for all
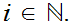
A Metric Space,
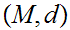 is
called
is
called
limit compact if every infinite subset
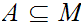 has
a limit point.
has
a limit point.
sequentially compact if Every sequence in
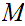 has a convergent subsequence. That is given
has a convergent subsequence. That is given

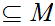 we can find a subsequence
we can find a subsequence
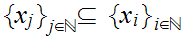
countably compact if every covering
 by a countable number of open sets ,
by a countable number of open sets ,
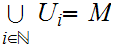 ,
contains a finite subcover. That is there is some finite subset
,
contains a finite subcover. That is there is some finite subset
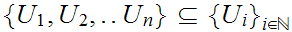 such that
such that
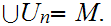
"totally"(my term) compact if every covering
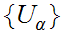 by a open sets contains a finite subcover.
by a open sets contains a finite subcover.
For Metric Spaces these four forms of compactness are equivalent.
In General Topology these four forms of compactness are not equivalent.
Given a sequentially/limit compact Metric Space
 and a covering
and a covering
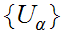 by open sets
by open sets
(
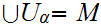 ),
there exists a real number
),
there exists a real number
 such that every open ball of radius
such that every open ball of radius
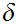 is contained in some element of
is contained in some element of
 .
.
The number
 is called a Lebesgue number for the covering.
is called a Lebesgue number for the covering.
Given
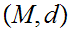 a Metric Space, a function
a Metric Space, a function
 is said to be a contraction mapping if there is a constant
is said to be a contraction mapping if there is a constant
 with
with
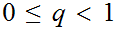 such that for all
such that for all
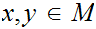
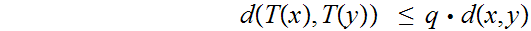
Let
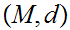 be a complete metric space then every contraction has a unique fixed point.
be a complete metric space then every contraction has a unique fixed point.
Proof:
*

Thus
 is Cauchy. Moreover we can use * to estimate the
limit.
is Cauchy. Moreover we can use * to estimate the
limit.
Let
 be a sequence of continuous functions for a metric space
be a sequence of continuous functions for a metric space
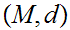 to a metric space
to a metric space
 . The sequence is said to converge uniformly to
. The sequence is said to converge uniformly to
 if
for any
if
for any
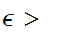 0
, there is a n such that
0
, there is a n such that
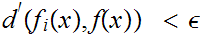 for all
for all
 and i
and i
 n
.
n
.
We write
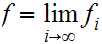 .
.
In the setting of 25.1,
 is continuous. That is the limit of a uniformly convergent sequence of
continuous functions is continuous.
is continuous. That is the limit of a uniformly convergent sequence of
continuous functions is continuous.
Given a Metric Space
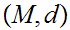 we let
we let
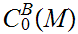 be the set of bounded real valued continuous functions on
be the set of bounded real valued continuous functions on
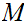 .
For
.
For
 , define
, define

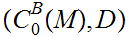 is a complete Metric Space.
is a complete Metric Space.
There is an isometric embedding

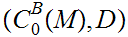 .
.
Proof:
Fix
 and
for all
and
for all
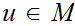 define
define
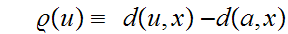
Topological Properties
|
Metric Properties
| |
|
_________________
|
_________________
| |
|
The Category of Metric Spaces and Continuous Maps
|
The Category of Metric Spaces and Uniformly Continuous Maps
| |
|
________________
|
_________________
| |
|
Continuous maps preserve limits
|
Uniformly continuous maps preserve limits
| |
|
________________
|
_________________
| |
|
Continuous maps MAY NOT preserve Cauchy sequences
|
Uniformly continuous maps preserve Cauchy sequences
| |
|
________________
|
_________________
|