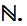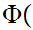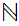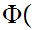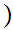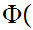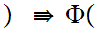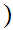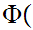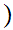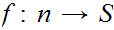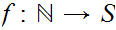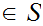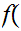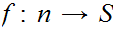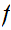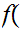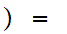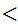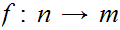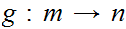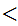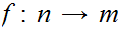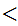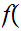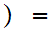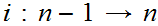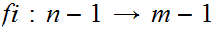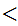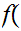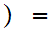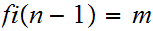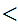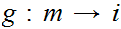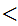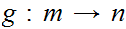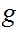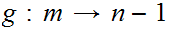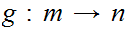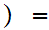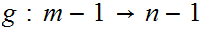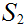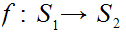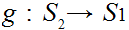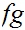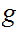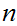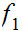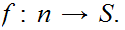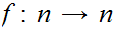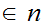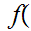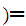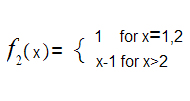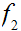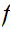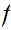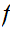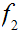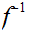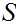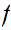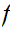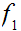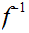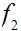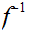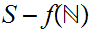5. Set Theory for the Natural Numbers - Cardinality
.
Set Theory for Working Mathematicians:
For the most part, working mathematicians take an informal point of
view about Set Theory, as if the
Tentative Definition presented
earlier was not as problematic as in fact they know it to
be. However, when proper care is exercised, this provides a
more manageable framework for mathematical discourse than strict adherence to
the formalism of Axiomatic Set Theory. This is the point of
view that we will take for the remainder of this course. In the same vein, we
will also use the terms such as "function" ("map"), "union", "intersection",
"empty set", etc. with their usual informal meaning.
We begin the discussion of this "Informal Set Theory" by reviewing the Set
Theory of finite Sets
and 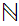 ,
the Natural numbers. The Natural numbers will provide a foundation
for our general considerations about sets because many of the issues that we
will have to consider appear as soon as one passes from the finite subsets
of
,
the Natural numbers. The Natural numbers will provide a foundation
for our general considerations about sets because many of the issues that we
will have to consider appear as soon as one passes from the finite subsets
of 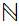 to
to
 itself,
beginning with the measurement of the size of a Set. We use the following,
itself,
beginning with the measurement of the size of a Set. We use the following,
Notation:
We use the symbol
 to denote the subsets
{1,2,....,n} of
to denote the subsets
{1,2,....,n} of
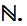
Mathematical Induction for the Natural Numbers :
Suppose that we have a proposition
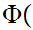 n
n on
on
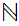 .
Suppose
.
Suppose
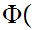 1
1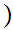 is true and
is true and
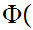 n
n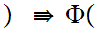 n+1
n+1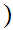 is true for all n. Then,
is true for all n. Then,
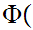 n
n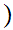 is true for all n.
is true for all n.
Here is a link to
Doctor
Hilary Priestley's notes on Set Theory which he has been kind enough
to make available for this course.
Measurement
by Cardinality:
5.1 Lemma:
Let
 be a given set. Either, for some n there exists a 1 to 1 and
onto function
be a given set. Either, for some n there exists a 1 to 1 and
onto function
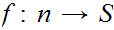 , or there exists a 1 to 1 function
, or there exists a 1 to 1 function
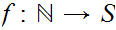 .
.
Proof:
This is a simple induction argument. Pick some
x 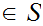 and define
and define
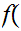 1
1 x
x Suppose we have defined a 1 to 1 function
Suppose we have defined a 1 to 1 function
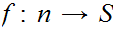 ,if
,if
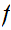 is
onto we are done, if not we can extend it to
is
onto we are done, if not we can extend it to
 by defining
by defining
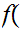 n+1
n+1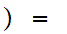 y
y
 .
.
5.2 Lemma:
Let n
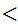 m. There does not exist an onto function
m. There does not exist an onto function
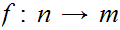 .
There does not exist
.
There does not exist
a 1 to 1 function
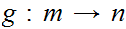 .
.
Proof:
The proofs of the two statements are simple induction arguments.The first, is
an induction on
 .
.
Clearly if 1
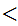 m there are no onto functions
m there are no onto functions
 .
Now suppose we know this holds for
n-1 Assume we have
.
Now suppose we know this holds for
n-1 Assume we have
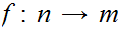 onto with n
onto with n
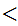 m. By permuting
m. By permuting
 we can assume
we can assume
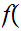 n
n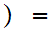 m.
m.
Consider the inclusion
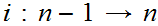 and the composition
and the composition

There are two cases to consider. Either
 is onto or
is onto or
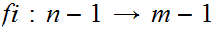 is onto. (Why?)
is onto. (Why?)
In either case, this is not possible by induction. The proof of the second
statement similar, beginning the induction with
 .
.
Assignment:
Complete the Proof. (To be turned in Feb. 2.)
Solution:
Either
 is onto or
is onto or
 is onto because either there is some i
is onto because either there is some i
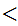 n with
n with
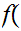 i
i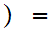 m
in which case
m
in which case
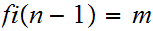 or
or

To prove the second statement.
If 1
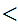 m there are no one to one functions
m there are no one to one functions
 .
.
Next suppose there are no one to one functions
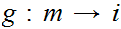 for i
for i
 m and i
m and i
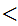 n. Assume we are given a one to one function
n. Assume we are given a one to one function
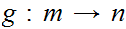 with n
with n
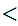 m. By induction we can assume that
m. By induction we can assume that
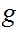 is onto since if i
is onto since if i
 we
can transpose i and n to give
we
can transpose i and n to give
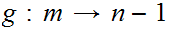 one to one which contradicts the induction hypothesis.
one to one which contradicts the induction hypothesis.
Hence
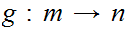 is 1 to 1 and onto. Again, by a transposition, we can assume
is 1 to 1 and onto. Again, by a transposition, we can assume
 m
m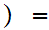 n
but again since is one to one
n
but again since is one to one
so is
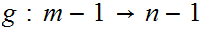 ,again a contradiction.
,again a contradiction.
5.3 Definition: A Set,
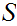 is said to be "finite" if every function
is said to be "finite" if every function
 is onto iff it is 1 to 1.
is onto iff it is 1 to 1.
5.4 Theorem:
Suppose I have two finite sets
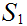 and
and
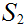 and 1 to 1 maps
and 1 to 1 maps
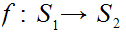 and
and
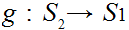 , then
, then
 and
and
 are also onto.
are also onto.
Proof:
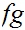 is a 1 to 1 self-map for a finite set, hence it is onto. So
is a 1 to 1 self-map for a finite set, hence it is onto. So
 must be onto. Similarly since
must be onto. Similarly since
 is a 1 to 1 self-map,
is a 1 to 1 self-map,
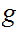 must be onto.
must be onto.
5.5 Theorem:
The following three statements are true:
-
The subsets
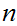 are finite.
are finite.
-
There exist functions
 such that
such that
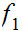 is 1 to 1 but not onto and
is 1 to 1 but not onto and
 is
onto but not 1 to 1.
is
onto but not 1 to 1.
-
Let
 be a finite set, then there exists an
be a finite set, then there exists an
 and a 1 to 1 onto function
and a 1 to 1 onto function
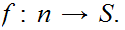
Proof:
1. Suppose that we have a 1 to 1 function
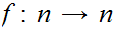 that is not onto. Again, by permuting the range we can assume that there does
not exist an
m
that is not onto. Again, by permuting the range we can assume that there does
not exist an
m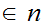 with
with
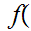 m
m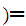 n. Hence, we can assume we have a 1 to 1 function
n. Hence, we can assume we have a 1 to 1 function
 contradicting 5.2 . More or less the same argument
works for
contradicting 5.2 . More or less the same argument
works for
 onto but not 1 to 1.
onto but not 1 to 1.
2. Let
 x
x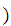 =
x+1 and
=
x+1 and
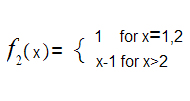
3. Restating 5.1, either one
can find some 1 to 1 onto function
 ,or, by induction one can construct a
,or, by induction one can construct a
1 to 1 function
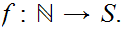 Letting
Letting
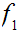 and
and
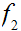 be
the functions defined in 2. above, if
be
the functions defined in 2. above, if
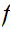 is also onto then
is also onto then
use
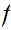

 or
or
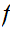
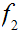
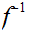 to
show that
to
show that
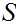 is not finite. If
is not finite. If
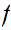 is not onto, the previous argument still works extending
is not onto, the previous argument still works extending
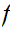
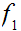
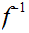 or
or

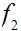
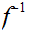 to all of
to all of
 by defining it to be the identity map on
by defining it to be the identity map on
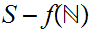 .
.
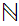 ,
the Natural numbers. The Natural numbers will provide a foundation
for our general considerations about sets because many of the issues that we
will have to consider appear as soon as one passes from the finite subsets
of
,
the Natural numbers. The Natural numbers will provide a foundation
for our general considerations about sets because many of the issues that we
will have to consider appear as soon as one passes from the finite subsets
of 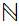 to
to
 itself,
beginning with the measurement of the size of a Set. We use the following,
itself,
beginning with the measurement of the size of a Set. We use the following,