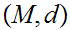 and a point
and a point

Fix a Metric Space
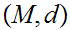 and a point
and a point

Given
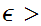 0
we define the open ball of radius
0
we define the open ball of radius
 around
around
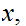

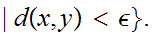
We say
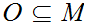 is open if for any
is open if for any
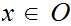 there exist an
there exist an
 0
such that
0
such that
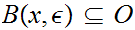
The set of open sets is called the Topology defined by the Metric.
In a Metric Space

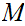 and
and
 (the empty set) is open
(the empty set) is open
Let
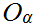 be an arbitrary set of open sets, then
be an arbitrary set of open sets, then
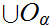 is
also open.
is
also open.
Let
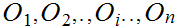 be
a finite set of open sets, then
be
a finite set of open sets, then
 is
also open.
is
also open.
1. and 2. follow directly from the definitions, however if you haven't been through this material you should write down the details.
3. makes use of the observation that if
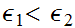 then
then
 .
Choose
.
Choose
 . Let
. Let
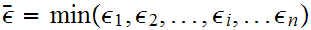 . We have
. We have
 for all
for all
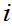 hence
hence
 .
.
18.2.1 Exercise: Show that
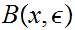 is open for any
is open for any
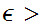 0.
0.
Solution:
For every
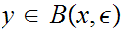 . We need to find some
. We need to find some
 0
such that
0
such that
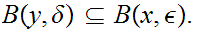 Let
Let
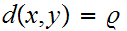 and
and
 For
every
For
every
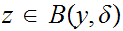 . We have
. We have
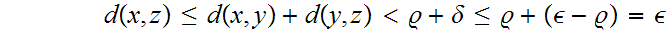 .
.
Thus
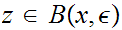 since this is true for any
since this is true for any
 we have
we have
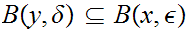
Given Metric Spaces
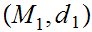 ,
,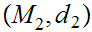 and a function
and a function
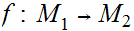 .
We say that
.
We say that
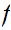 is continuous a point
is continuous a point
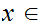
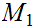 if given any
if given any
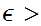 0
there is a
0
there is a
 0
such that
0
such that
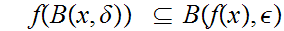 .
.
We say that
 is continuous if it is continuous at every point.
is continuous if it is continuous at every point.
Exercise: Convince yourself that for
 this is just the usual
this is just the usual
 definition.
definition.
Given Metric Spaces
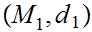 ,
,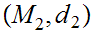 ,a function
,a function
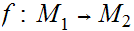 is continuous if and only for every open set
is continuous if and only for every open set
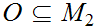
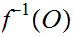 is open in
is open in
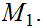
Proof:
Assignment: To be turned in one week from today.
Solution:
Suppose for every open set
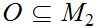 we know that
we know that
 is open in
is open in
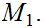 Suppose we are given
Suppose we are given
 0
and
0
and

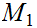 .
We need to find
.
We need to find
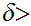 0
such that
0
such that
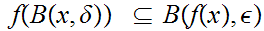 .
But by 18.2.1 we know that
.
But by 18.2.1 we know that
 is open. Hence
is open. Hence
 is open. Hence we can find
is open. Hence we can find
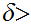 0
such that
0
such that
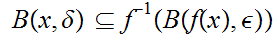 . Or, equivalently,
. Or, equivalently,
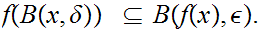
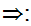
Suppose
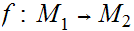 is continuous and
is continuous and
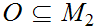 is open we need to show that
is open we need to show that
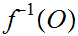 is open in
is open in
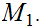 Suppose
we are given
Suppose
we are given
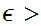 0
and
0
and

 such that
such that
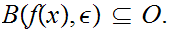 Since
Since
 is continuous, we can find
is continuous, we can find
 0
such that
0
such that

 Thus
Thus
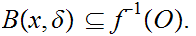
Suppose we have two metrics
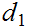 and
and
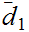 defined
on
defined
on
 that produce the same Topology (open sets). Then a function
that produce the same Topology (open sets). Then a function
 is continuous with respect to the metric
is continuous with respect to the metric
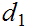 if and only if it is continuous with respect to the metric
if and only if it is continuous with respect to the metric
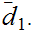
Exercise: State and prove the corresponding
appropriate result for
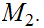
Suppose we have three Metric Spaces
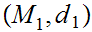 ,
,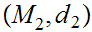 , and
, and
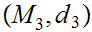 suppose
suppose
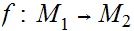 and
and
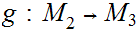 are continuous, then so is
are continuous, then so is
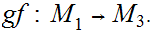
Proof:
Let
 be open. Since
be open. Since
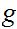 is continuous so is
is continuous so is
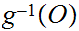 is open in
is open in
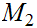 and since
and since
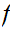 is continuous
is continuous
so is

Given Metric Spaces
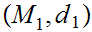 ,
, we use the notation
we use the notation
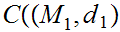 ,
,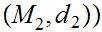 to represent the set of continuous functions from
to represent the set of continuous functions from
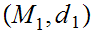 to
to
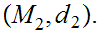
Let
 be a metric space and
be a metric space and
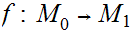 be a continuous function from
be a continuous function from
 to
to
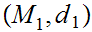 , then
, then
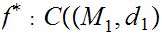 ,
,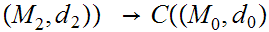 ,
,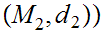
where, as in 0.1,
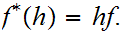
Let
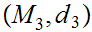 be a metric space and
be a metric space and
 be a continuous function from
be a continuous function from
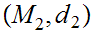 to
to
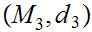 ,
then
,
then
 ,
,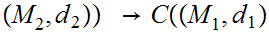 ,
,
where

Proof: Immediate from 18.5
Returning to 17.3 The Circle,
 we want to show that the three Metrics
we want to show that the three Metrics

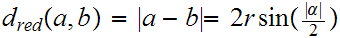
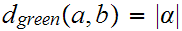
produce the same set of continuous functions.
Assignment: (To be turned in one week from today) We could simply use 18.4 (do this!)
Solution:
We need to show that
 is open with respect to
is open with respect to
 iff it is open with respect to
iff it is open with respect to
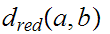 iff
it is open with respect to
iff
it is open with respect to

To accomplish this, it suffices to show that if we are given
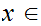
 and
and
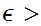 0
we can find, in sequence
0
we can find, in sequence
 0
,
0
,  0
and
0
and
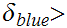 0
such that
0
such that
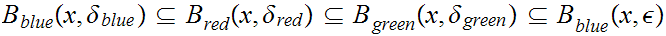
One note: there is no loss of generality in assuming that the
 or
or
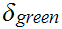 we work with for the next computation are smaller than the one we initially
are given, or compute.
we work with for the next computation are smaller than the one we initially
are given, or compute.
Beginning with a simple case, let
 Suppose
we know that
Suppose
we know that
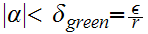 then we know
then we know
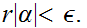
So
 .
.
The hardest calculations involve
 . Given
. Given
 0
, I need find
0
, I need find
 0
0

In computing
 we make use of the inequality
we make use of the inequality
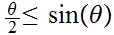 for small positive values of
for small positive values of
 .
.
Let
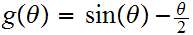
then
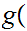 0
0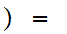 0
and
0
and
 0
for small
0
for small

Now let
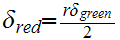 . Suppose
. Suppose

we have
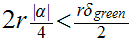 or
or
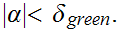
The computation of
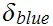 follows in a similar fashion using the observation that
follows in a similar fashion using the observation that
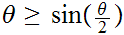 for
for
 0.
0.
Let
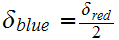 and assume that
and assume that
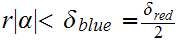 ,
we have
,
we have
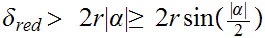
but it will be useful in the sequel if we go about it in a slightly different way.
The identity map
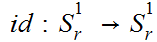 is continuous with respect to any pair of the above Metrics.
is continuous with respect to any pair of the above Metrics.
Proof:
Using
 to denote the identity map when considered as a map between specific Metric
spaces, it is sufficient to show
to denote the identity map when considered as a map between specific Metric
spaces, it is sufficient to show

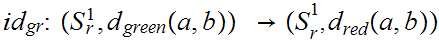
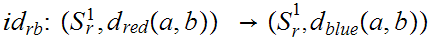
are continuous since for example,
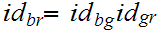 is continuous by 18.5. Since all three arguments are
similar we give the details of 1. Choose
is continuous by 18.5. Since all three arguments are
similar we give the details of 1. Choose
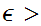 0
and
0
and
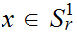 .
Let
.
Let
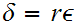 . Suppose
. Suppose
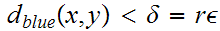 .
.
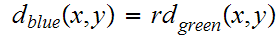 we have
we have
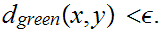 For
large radii points can be far apart in distance yet close in terms of angle.
For
large radii points can be far apart in distance yet close in terms of angle.
Let
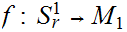 be a map of sets. suppose
be a map of sets. suppose
 is equipped with a Metric
is equipped with a Metric
 .
Then if
.
Then if
 is continuous with respect to any of the three metrics
is continuous with respect to any of the three metrics
 is continuous with respect to the other two.
is continuous with respect to the other two.
Proof:
Suppose
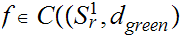 ,
,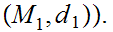
As a set map
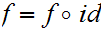 on the other hand, by 18.7
on the other hand, by 18.7
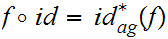 is continuous for
is continuous for
