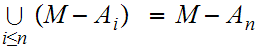23.1 Definition:
Given a Metric Space
 ,
and a subset
,
and a subset
 we
say
we
say
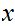 is
a limit point of
is
a limit point of
 if
if
___________
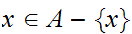
That is
 is
in the closure of
is
in the closure of
Notes:
The definition does not claim
that
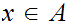
It is not necessarily the case that the set of limit points of
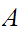 is
the closure of
is
the closure of
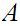 .
For example, a singleton set
.
For example, a singleton set
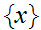 has no limit points but is its own closure.
has no limit points but is its own closure.
Remember,
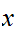 is
in the closure of
is
in the closure of
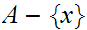 means that for any
means that for any
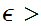 0
0
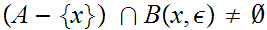
23.2 Definitions:
A sequence in
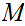 is just a map
is just a map
 Notationally
Notationally

Given a one to one order preserving map
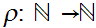 ,
the map
,
the map
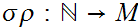
is called a subsequence. We will usually just write "
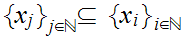 is a subsequence."
is a subsequence."
A covering
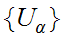 of
a Set M is a collection of subsets such that
of
a Set M is a collection of subsets such that
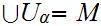 .
.
23.3 Definition:
A Metric Space,
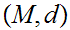 is
called
is
called
limit compact if every infinite subset
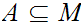 has
a limit point.
has
a limit point.
sequentially compact if Every sequence in
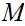 has a convergent subsequence. That is given
has a convergent subsequence. That is given
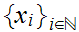
 we can find a subsequence
we can find a subsequence
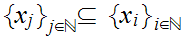
countably compact if every covering
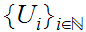 by a countable number of open sets ,
by a countable number of open sets ,
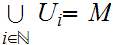 ,
contains a finite subcover. That is there is some finite subset
,
contains a finite subcover. That is there is some finite subset
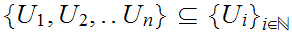 such that
such that
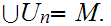
"totally"(my term) compact if every covering
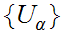 by a open sets contains a finite subcover.
by a open sets contains a finite subcover.
23.4 Theorem:
For Metric Spaces these four forms of compactness are equivalent.
In General Topology these four forms of compactness are not equivalent.
Proof:
1.
 2.
This is 21.4.
2.
This is 21.4.
We will not present counter-examples to the general theorem.
The remainder of this Page is devoted to completing the proofs of the various equivalences.
21.4.1 Corollary:
Every sequentially/limit compact Metric Space is complete:
21.5 Theorem:
Given a sequentially/limit compact Metric Spaces
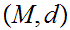 :
:
For any
 0
and some
n
0
and some
n there exists points
there exists points

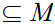
such that
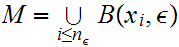 .
.
In particular, M is bounded in the sense that there exists some
b 0
such that
0
such that
 b for
any
b for
any
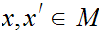 .
.
21.6 Theorem(Restated):
Every sequentially/limit compact metric space has a countable dense subset.
Given a sequentially/limit compact Metric Space
 and a covering
and a covering
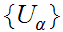 by open sets
by open sets
(
 ),
there exists a real number
),
there exists a real number
 such that every open ball of radius
such that every open ball of radius
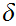 is contained in some element of
is contained in some element of
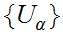 .
.
The number
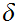 is called a Lebesgue number for the covering.
is called a Lebesgue number for the covering.
Proof:
Suppose that no Lebesgue number existed. Then there exists an open cover
 such that for all
such that for all
 there exists an
there exists an
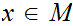 such that
no
such that
no 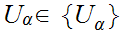 contains
contains 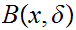 . In
particular for each n we can choose a sequence
. In
particular for each n we can choose a sequence
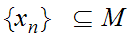 such
that
such
that
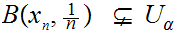 for
any
for
any
 .
.
The proof continues in the same way as several of the proofs on Page 21:
Since
 is compact choose a convergent subsequence
is compact choose a convergent subsequence
 with
with
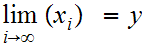 for some
for some
 .
Since
.
Since
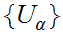 is an open cover, we know there is some
is an open cover, we know there is some
 and some
and some
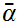 with
with
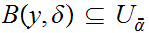 .
Again, as before, choose n such that
.
Again, as before, choose n such that
 and
and
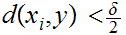 for
i
for
i 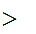 n.
Check that
n.
Check that

Every open covering,
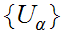 of a compact Metric Space
of a compact Metric Space
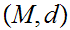 has a finite subcovering. In particular 1.
has a finite subcovering. In particular 1.
 2.
2. 4.
4. 3.
3.
Proof:
Let
 be a Lebesgue number for
be a Lebesgue number for
 .
Applying 21.5, we know there is some
.
Applying 21.5, we know there is some
n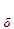 and points
and points

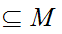 such
that
such
that
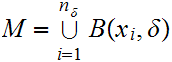 .
But since
.
But since
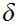 is
a Lebesgue number for each i we can find
is
a Lebesgue number for each i we can find
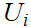 such
that
such
that
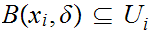 and
hence
and
hence

Let
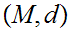 be
countabily compact, then every infinite set contains a limit point. In
particular,
3.
be
countabily compact, then every infinite set contains a limit point. In
particular,
3. 1.
Hence, 1.
1.
Hence, 1.
 2.
2.
 3.
3.
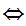 4.
4.
Let
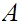 be an infinite subset of
be an infinite subset of
 without limit points, then . Without loss of generality we can assume that
without limit points, then . Without loss of generality we can assume that
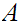 is countable. Writing
is countable. Writing
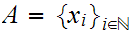 , and
, and
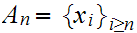
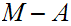 is open since
is open since
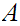 has no limit points. More generally
has no limit points. More generally
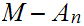 is open. One notes that,
is open. One notes that,
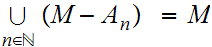
and
There is no finite subset that covers
 . In particular,
. In particular,