 in a Metric Space
in a Metric Space
 is called a Cauchy Sequence
is called a Cauchy Sequence
20.1 Definition:
A sequence
 in a Metric Space
in a Metric Space
 is called a Cauchy Sequence
is called a Cauchy Sequence
if for any
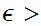 0 there
exists an
n
0 there
exists an
n such that if
such that if
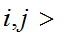 n
n then
then

20.2 Lemma:
In the setting of 20.1 , every Cauchy sequence is
bounded. In particular there is a number
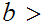 0
and
an
0
and
an 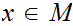 such that
such that
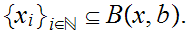
Proof:
Select
n such that if
such that if
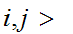 n
n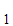 then
then
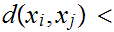 1.
Now let
1.
Now let
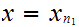 and select any
and select any
 1
1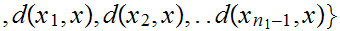
20.3 Lemma:
In the setting of 20.1 , if
 then
then
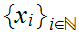 is a Cauchy Sequence.
is a Cauchy Sequence.
Proof:
This quickly follows from the observation that
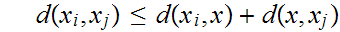
hence if
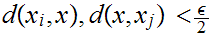 then
then

20.4 Examples and Observations:
In general, the converse to 20.3 is not true.
Consider, for example, the open interval
 0,1
0,1 and the sequence
and the sequence
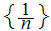 clearly
is Cauchy but does not have a limit.
clearly
is Cauchy but does not have a limit.
It is also the case that Cauchy sequences are not preserved under mapping by
continuous functions. For example, consider
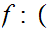 0,1
0,1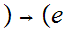 ,
,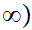 given by
given by
 and
the Cauchy sequence
and
the Cauchy sequence
 .
.
on the other hand
In
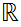 , every Cauchy sequence converges.
, every Cauchy sequence converges.
Proof:
Since
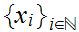 is bounded, so is
is bounded, so is
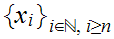 .
let
.
let
 and
and
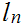 be the greatest lower bound and least upper bounds respectively. On checks
that
be the greatest lower bound and least upper bounds respectively. On checks
that

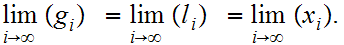
Assignment: Due April 13 . Fill in the details.
20.5 Definition:
A Metric Space is called complete if every Cauchy sequence converges. In particular,
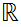 is a complete metric space.
is a complete metric space.
20.6 Theorem:
Let
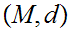 be a complete Metric Space and let
be a complete Metric Space and let
 be closed, then
be closed, then
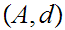 is a complete Metric Space.
is a complete Metric Space.
Proof:
Any Cauchy sequence in
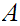 converges
in
converges
in
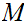 ,
but
,
but
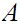 is
closed so it contains all its limit points.
is
closed so it contains all its limit points.
20.7 Theorem:
Given Metric Spaces
 and
and
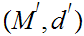 , we can define a metric
, we can define a metric
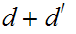 on
on
 by setting
by setting
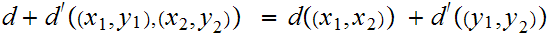
Then if
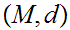 and
and
 are complete so is
are complete so is
 .
.
Proof:
After checking that is a
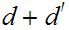 metric,
the essential point is the proof is to show that if
metric,
the essential point is the proof is to show that if
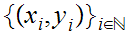 is a Cachy sequence for
is a Cachy sequence for
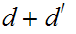 then
so is
then
so is
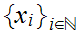 and
and
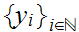 for
for
 and
and
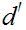 respectively.
Hence
respectively.
Hence
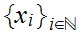 and
and
 converge to
converge to
 and
and
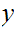 respectively. Finally,
respectively. Finally,
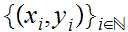 converges to
converges to
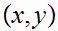 .
.
Assignment: Due April 13 . State and prove the converse.
We would like to discuss the Category of Complete Metric Spaces. Unsettled is the appropriate choice of morphisms. Since we wish these to be structure preserving 20.4.1 tells us that continuous functions might be a poor choice since, in general, they do do preserve Cauchy sequences. There is an important sub-class of continuous functions which do preserve Cauchy sequences and, in fact, are the continous functions on an important sub-Category of Complete Metric Spaces.
20.8 Definition:
Given Metric Spaces
 and
and
 and a map
and a map
 we say that
we say that
 is
is
uniformly continuous if for all
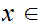
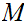 ,given any
,given any
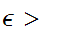 0
there is a
0
there is a
 0
such
that
0
such
that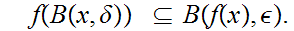 Note
that this differs for continuity in that
Note
that this differs for continuity in that
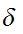 is
independent of
is
independent of
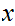 .
.
Remarks:
We will show, for example, that every continuous function
 0,1
0,1 0,1
0,1![$\QTR{Large}{]}$](graphics/Cauchy__79.png) is uniformly continuous.
is uniformly continuous.
To verify that complete metric spaces and uniformly continuous maps form a category we need to check the the composition of uniformly continuous maps is uniformly continuous.
20.9 Theorem:
In the setting of 20.8, if
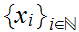 is a Cauchy sequence in
is a Cauchy sequence in
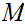 then
then
 is a Cauchy sequence in
is a Cauchy sequence in
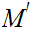 .
.
Proof:
Given
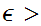 0 we
need to find
n
0 we
need to find
n such that if
such that if
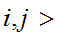 n
n then
then

But since is uniformly continuous we can choose
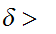 0
such
that
0
such
that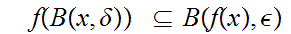 for
all
for
all
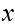 .
Select
n
.
Select
n such that if
such that if
 n
n then
then
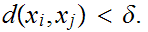
We will also want to look at the following uniformly continuous functions.
20.10 Definition:
Given Metric Spaces
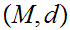 and
and
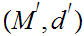 ,a map
,a map
 is said to be an isometry if for all
is said to be an isometry if for all
 ,
,
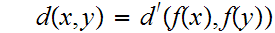
Given Metric Spaces
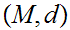 one first observes that if
0
one first observes that if
0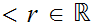 then
then
 is also a Metric Space
is also a Metric Space
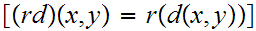 .
Moreover the two Metric Spaces have the same Cauchy Sequences.
.
Moreover the two Metric Spaces have the same Cauchy Sequences.
In the setting of 1., Given a second metric
 such that for all
such that for all
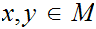 we
have
we
have
then
 and
and
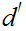 have the same Cauchy Sequences.
have the same Cauchy Sequences.