 a Metric Space, a function
a Metric Space, a function
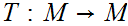 is said to be a contraction mapping if there is a constant
is said to be a contraction mapping if there is a constant
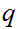 with
with
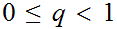 such that for all
such that for all
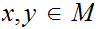
The Banach Fixed Point Theorem is a very good example of the sort of theorem that the author of this quote would approve. The theorem and proof:
Tell us that under a certain condition there is a unique fixed point.
Tell us that the fixed point is the limit of a certain computable sequence.
Give us an estimate of how close each term of the sequence is to the fixed point.
Given
 a Metric Space, a function
a Metric Space, a function
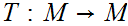 is said to be a contraction mapping if there is a constant
is said to be a contraction mapping if there is a constant
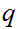 with
with
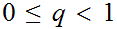 such that for all
such that for all
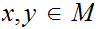

.
Let
 be a complete metric space then every contraction has a unique fixed point.
be a complete metric space then every contraction has a unique fixed point.
Proof:
That the fixed point is unique follows from the observation that if
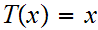 and
and
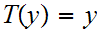
then
 ,
but
,
but
 so
so
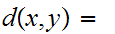 0
0 or
or
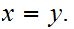
To show that a fixed point exists, pick any
 . Setting
. Setting
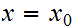 we define a sequence
we define a sequence
 by setting
by setting

Rewriting the contraction formula we have

or
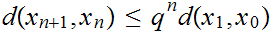
Finally, assuming n
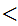 m
m
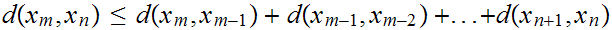

or
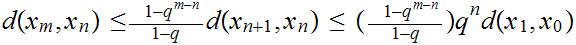
and since
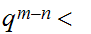 1
1
*
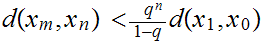
Thus
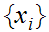 is Cauchy. Moreover we can use * to estimate the
limit.
is Cauchy. Moreover we can use * to estimate the
limit.
There are any number of important applications of The Banach Fixed Point Theorem. The text discusses one. Unfortunately, we will not have time to discuss any of them this semester. The following example, is just meant to give a taste of how the theorem is used.
Let
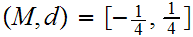 with the standard metric. Let
with the standard metric. Let

Since
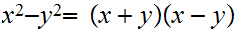
 on
on
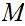
It is indeed the case that for
any
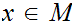 we have
we have
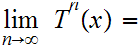 0.
0.
Note that on
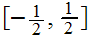 ,
,
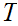 also has a unique fixed point.
also has a unique fixed point.