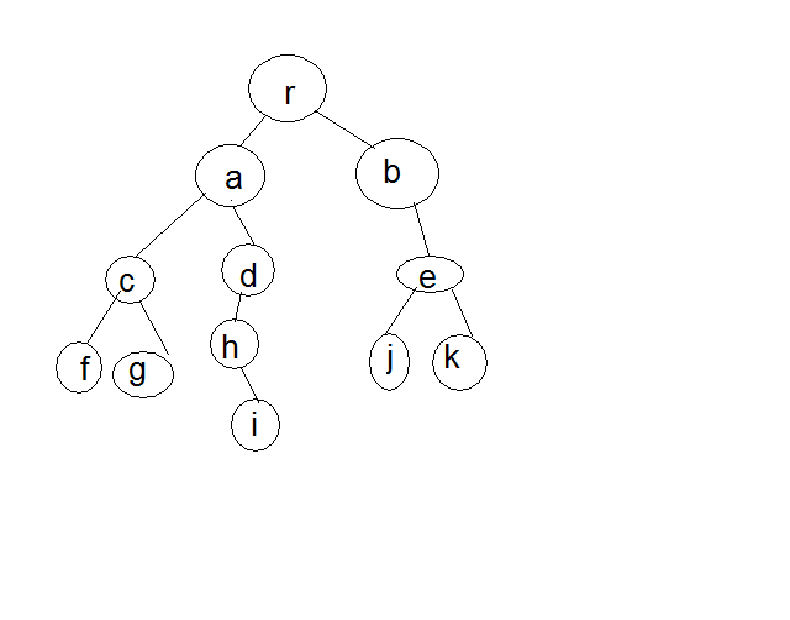
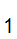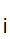There is a distinguished node n
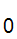 , called the "root".
, called the "root".
( child(n))
child(n))
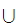 {n
{n
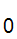 }
}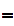 N
N
 child(n
child(n
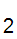 )
)
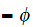
The set of nodes with child(n)
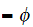 is called the set of "leaves".
is called the set of "leaves".
We will use the notation N for the set of nodes and the tree
interchangeably. We will use N