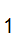 ,x
,x
 )
that returns a 1 if the program x
)
that returns a 1 if the program x
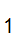 stops on x
stops on x
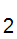 and returns 0 when x
and returns 0 when x
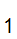 does
not stop(infinite loop) on x
does
not stop(infinite loop) on x
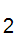 .
That is f(x
.
That is f(x
 )
returns a value or f(x
)
returns a value or f(x
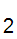 )
does not return.
)
does not return.
The Stopping Problem - Can you write a program that checks other programs for infinite loops?
Remembering that the representation of a program, within a large computer is just a "large integer," we will work with integer psudo-programming language anduse a C-like functional programming notation
f(x){
//C expressions and statements.
return y; //x and y integers.
}
We write n(f)for the internal integer represention of f.
Theorem: There is no "program" stop(x
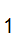 ,x
,x
 )
that returns a 1 if the program x
)
that returns a 1 if the program x
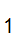 stops on x
stops on x
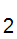 and returns 0 when x
and returns 0 when x
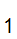 does
not stop(infinite loop) on x
does
not stop(infinite loop) on x
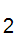 .
That is f(x
.
That is f(x
 )
returns a value or f(x
)
returns a value or f(x
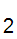 )
does not return.
)
does not return.
Proof:
Consider the program
f(x){
while(stop(x,x)==1){
continue;
}
return 2;
}
Compute stop(n(f),n(f)):
Suppose stop(n(f),n(f))=1. That is f(n(f)) stops. Looking at the program we see that this
is possible only if stop(n(f),n(f))=0.
Suppose stop(n(f),n(f))=0. That is f(n(f)) does not return. Looking at the program we see
that this means that f(n(f)=2. In particular it does return.
ÿ