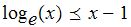 on
on
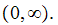
:
Since
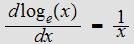
 for
for
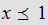
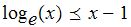 on
on
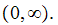
:
Since
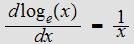
 for
for
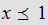
and
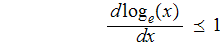 for
for

Hence
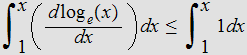
or

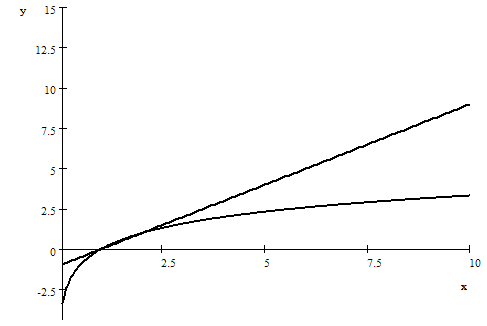
For
 ,
let
,
let
 and
and
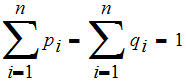
- 
:

Hence
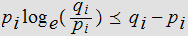
or
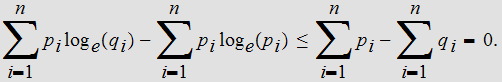
or
- 
Hence the result follows from the fact that
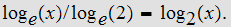 and
and

Application:
A binary cipher is said to be an instantaneous code if no ciphertext is a prefix of any other.
Here is an example of an instantaneous code
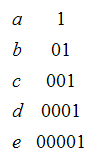
Here is an example of code that is not instantaneous.

It turns out that this second code is uniquely decipherable and the result we are about to consider holds for this class as well.
Let
( )
be an instantaneous code, where
)
be an instantaneous code, where
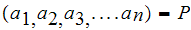 and
and
 .
Let
.
Let
 then
then

The proof can be visualized by looking at a tree diagram of the code
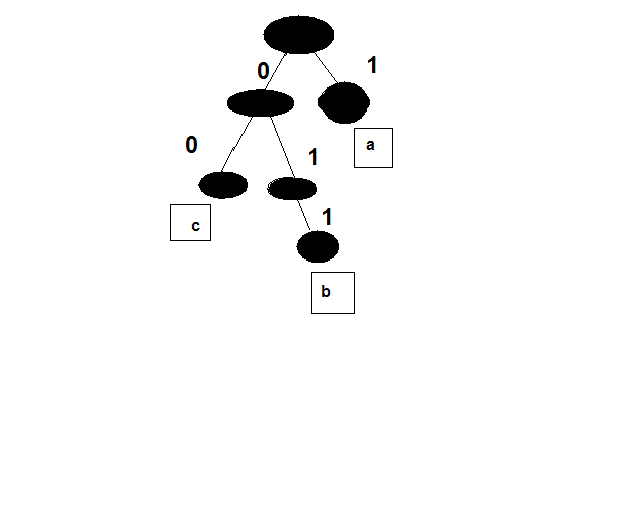
On can quickly prove that an instantaneous code has the property that all of its plaintext elements occur on the leafs of its tree. The proof is a simple induction on the depth of the tree.
: Let
(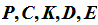 )
be an instantaneous code, where
)
be an instantaneous code, where
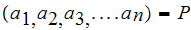 and
and
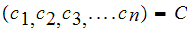 .
Let
.
Let
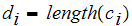 .
Finally let
.
Finally let
 be the probability that the plaintext
be the probability that the plaintext
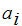 occurs in a message. Then
occurs in a message. Then

- 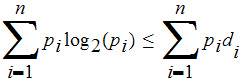
:
Choose
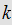 such that
such that
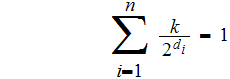 .
By the previous lemma we know that
.
By the previous lemma we know that
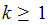 .
Setting
.
Setting
 we have
we have
 -
- 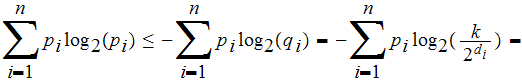
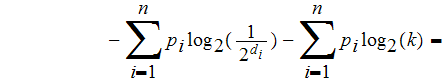

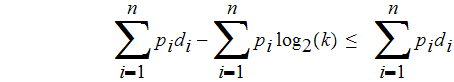 since
since
