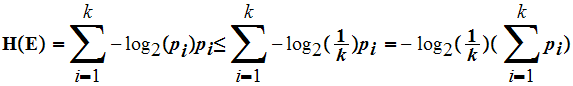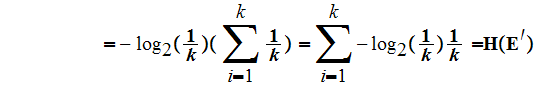Remember that we proposed that the Information should satisfy the following list of properties.
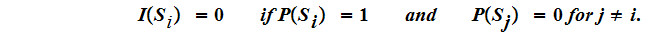

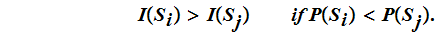
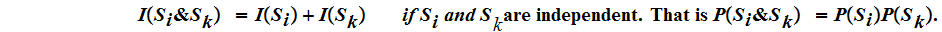
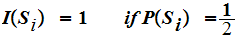
We want to show that
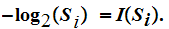 For our purposes we will content ourselves with the following
For our purposes we will content ourselves with the following
Let
 be
a differentiable function such that
be
a differentiable function such that
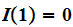
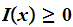
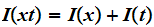
Then
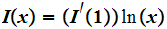
:
Considering
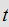 to be a constant and differentiating 3. we have
to be a constant and differentiating 3. we have
 or
or
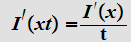 and setting
and setting
 we have
we have

The result now follow by Integrating both sides of the equation:
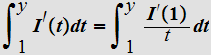 or
or

Since
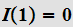 we have our result.
we have our result.
In point of fact we should be showing the uniqueness of the Entropy function, but we will simply define
If
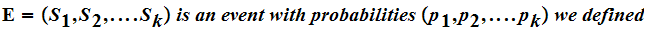

One intuitive concequence of the result of the last lecture is that we get the most information from an equiprobable event. That is if
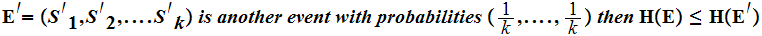
since