Notes from January 29

1. We considered possible interpretations of the word "information." We asked who has more information.

   A. The person who has knows someone's Public Key and that persons encrypted credit card number.

   B. The person who know 15 of the 16 digits in the same persons credit card number.

   We discussed that in the sense that A. provides complete information because someone who knows the Public Key and the encrypted

   credit card number can compute the credit card number can with no additional information! It may take 1000 years. B. can never discover the 16th digit without additional information even though there is only 10 choices.

2. We discussed the properties that an information function should have:

   

   

   

   

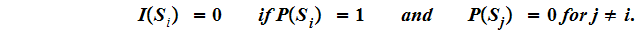
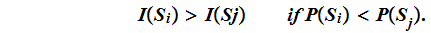
3. If we also require 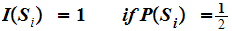then

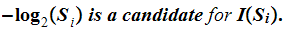
4. If

   

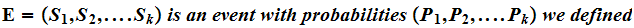
   to be the "Entropy" of the event, that the expected amount of information we expected to learn when we found out the outcome of the event.

   In the future we will write

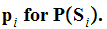
5. We discussed variable length binary codes and remarked that if is encoded with such a code that is uniquely decipherable then the

   Entropy is a lower bound for the expected length of a message. We also discussed Huffman encoding and mentioned that this actually gave a "best possible" uniquely decipherable code. We will return to this in detail over the next few lectures.