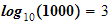Class Notes for January 20

1. • We considered the vague concept of "Work" it took to do a calculation. The basic idea was that if f(n) is some function then we considered that f was "computable" (by a computer) if the work it took to compute f(n) did not grow very fast, as n grew.

   • We looked at multiplication. The simplest template for multiplication (no carries) is

     x x x

             y y y

__________________

             z z z

           z z z

         z z z

________________________________

         w w w w

In particular, to multiply two numbers less than 1000 requires 3x3+4 calculations (again best case)

In general, remembering that 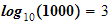we see that the work in doing multiplication's growth is related to

which is slow growing hence considered computable.

• We talked about the problem of factoring a product of two primes and discussed the fact that, today, this is not considered computable.

• We talked about computability of the Euclidean Algorithm, that is given 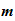and , finding 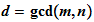,and and

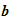
with

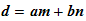
We assumed 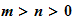and wrote the division algorithm as

and observed that

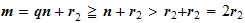
so

More generally,

In particular if

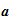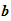We can comput the GCD in at most steps. The back substitution to compute and requires the same number of steps so the

Euclidean Algorithm requires work of the order of

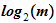
Again computable.