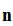 plaintext-probability pairs
plaintext-probability pairs
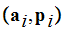 that is the probability that the symbol
that is the probability that the symbol
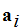 occurs in a message is
occurs in a message is
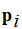 .
We also considered an instantaneous binary code
.
We also considered an instantaneous binary code
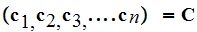 for
for
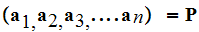 .
Finally we set
.
Finally we set
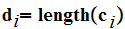
Reviewing, we considered a set
of
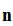 plaintext-probability pairs
plaintext-probability pairs
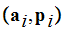 that is the probability that the symbol
that is the probability that the symbol
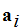 occurs in a message is
occurs in a message is
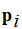 .
We also considered an instantaneous binary code
.
We also considered an instantaneous binary code
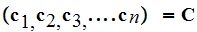 for
for
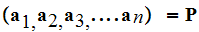 .
Finally we set
.
Finally we set
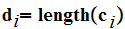
We were then able to show that
:

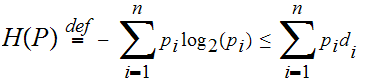
That is the expected length of
a coded symbol is bounded below by
 .
If I had a message
.
If I had a message
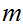 symbols of
symbols of
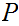 long and I encoded it using
long and I encoded it using
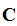 then
then
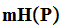 is a lower bound for the expected length of the coded message.
is a lower bound for the expected length of the coded message.
The key point in the proof was the observation that instantaneous codes were those where the code strings occur at the leaves of the binary tree representation of the code. Hence we have the formula.

One wants to know how to achieve the lower bound. In fact this is not
a "hard" problem like factoring primes. Brute force is even a viable method
(the number of interior nodes, relative to
 ,
of the trees we need to search can't get too big, why?). However there is a
rather simple algorithm to general a "best possible" code.
,
of the trees we need to search can't get too big, why?). However there is a
rather simple algorithm to general a "best possible" code.
At the root of Huffman's algorithm is a simple idea, which is...choose the longest binary string for the least probable symbol because this would reduce the expected length of a transmission.
That is:
if
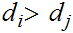 and
and
 then
then
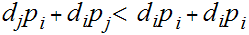 .
.
Hence
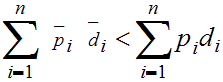 where the first summation is the result of interchanging
where the first summation is the result of interchanging
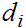 and
and
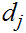 in the second.
in the second.
An Example: The idea of the algorithm is to build a tree from the leaves back towards the root. At each stage we "combine" the two least probable symbols, in effect adding a new node to the tree.
| a | .4 |
| b | .3 |
| c | .1 |
| d | .1 |
| e | .1 |
| a | .4 |
| b | .3 |
| de | .2 |
| c | .1 |
| a | .4 |
| b | .3 |
| cde | .3 |
| bcde | .6 |
| a | .4 |
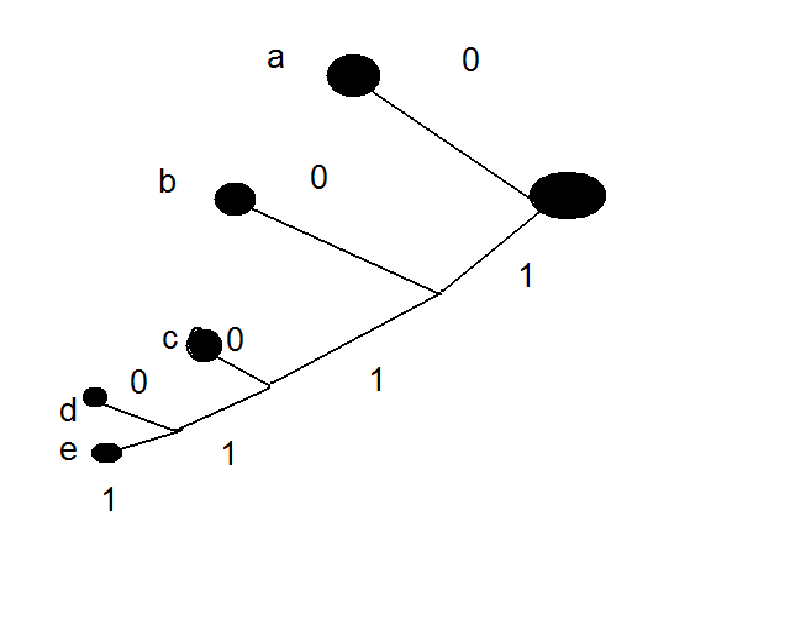
| a | 0 |
| b | 10 |
| c | 110 |
| d | 1110 |
| e | 1111 |
______________________________________________________________________________________________________
Suppose we have a cryptosystem.
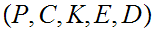 and an encrypted message
and an encrypted message
 the
big question is can we find the original plaintext message
the
big question is can we find the original plaintext message
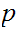 . Information Theory provide a general framework to study this and related
questions. Unfortunately the practical applications of this framework are
somewhat limited, at least for our purposes. On the other hand, it is
worthwhile to briefly review this area.
. Information Theory provide a general framework to study this and related
questions. Unfortunately the practical applications of this framework are
somewhat limited, at least for our purposes. On the other hand, it is
worthwhile to briefly review this area.
The first thing that must be done is to define
"Conditional Entropy." That is given events
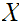 and
and
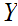 we want to consider
we want to consider
 the amount of uncertainty in
the amount of uncertainty in
 knowing after
knowing after
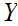 is revealed. The formula defining of
is revealed. The formula defining of
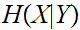 is an somewhat obvious extension of
is an somewhat obvious extension of
 . From the Information Theoretic point of view the
formulation involves the three sets
. From the Information Theoretic point of view the
formulation involves the three sets
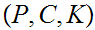 .
For example, the following definition:
.
For example, the following definition:
: We say
that a cryptosystem has perfect secrecy
if

In simple terms, the amount of uncertainty about a
message is the same whether or not we know the encrypted message. In order for
this definition to make sense we need to remember that for a message
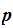 to be the plaintext of an encrypted message
to be the plaintext of an encrypted message
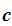 there needs to be some key
there needs to be some key
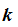 with
with
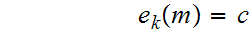
Examples:

Questions:
What about SHIFT and SUBSTITUTION Cyphers?
What about RSA?
Consider
 ,
remember that if I have an encrypted message and the Key that was used then I
can decode the message, is there a relationship between
,
remember that if I have an encrypted message and the Key that was used then I
can decode the message, is there a relationship between
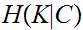 and
and
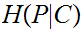 ?
?
In all the about we are more or less assuming that the distribution of plaintext messages are equiprobable. What role does the fact that we are dealing with natural languages play in this?