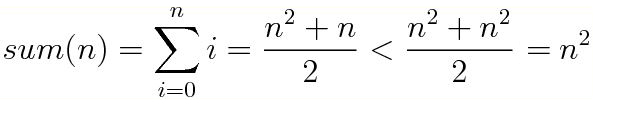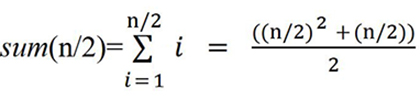Sorting
Some Mathematics
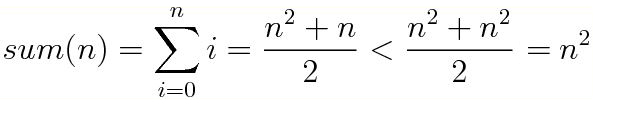
And
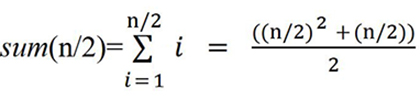
So, for our purposes (Some Details)
sum(n)≈4∗sum(n/2)
The Proof of the formula:
Add n+1 to both sides and note that
(n2+n)/2 + (n+1) = (n2+n)/2 + (2n+2)/2 =(n2+2n+1+n+1)/2 =((n+1)2+(n+1))/2
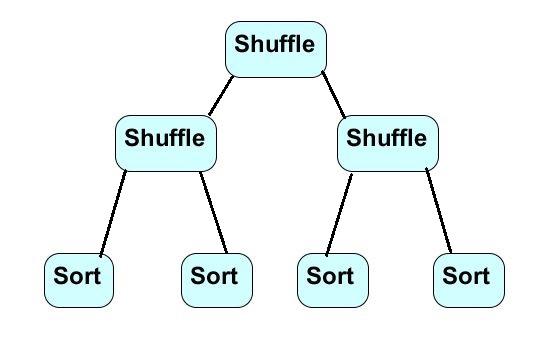
A Sketch of an Application - Sorting
Suppose we have a sequence of integers [a0,a1,...an] and
we want to sort them in increasing order. In the worst case it would take sum(n) comparisons. The list
was given to us in reverse order.
Alternatively, divide the list in half [a0,a1,...a(n/2)] and [(n/2)+1,a1,...an]
and sort each list in, worst case sum(n/2) comparisons. Then Shuffle the list together with (n/2) comparisons. The
smallest integer is the smallest of the two smallest on the two lists.
The Tree of Steps:
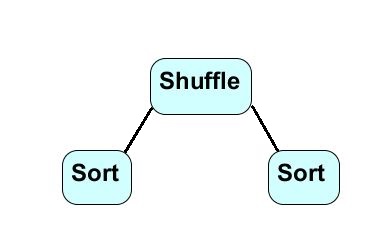
And divided into 4 lists: