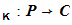 , and the general methodology used in its construction, did not lead to an
easy computation of d
, and the general methodology used in its construction, did not lead to an
easy computation of d
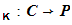 , then we could do the following.
, then we could do the following.
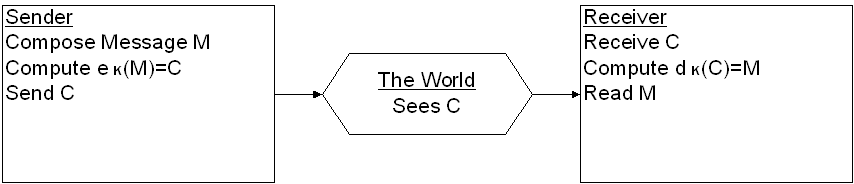
Definition:A cryptosystem is a five-tuple (P,C,K,E,D) where the following conditions are satisfied:
1. P is a finite set of possible plaintexts:
2. C is a finite set of possible ciphertexts:
3. K is the keyspace, is the a finite set of possible keys:
4. For each K∈ K there is an encryption rule eK∈E and a corresponding decryption rule dK∈D. Where
eK:P→C and dK:C→P are functions such that for all M∈P, we have dK(eK(M))=M
Caesar cipher- Shift K letters.
P and C are the alphabet. eK is shift K letters and dK is shift back K.
Alternative 1: Use permutations rather than shifts.
26! = 403291461126605635584000000
Alternative 2: Use a fixed sequence of Caesar_cipher shifts. Say (5,7,3).
The first letter gets shifted by 5,
the second by 7 and the third by 3. The fourth is again shifted by 5.
There are 26n possibilities for a sequence of n shifts.
For example, if n=30, there are 2813198901284745919258621029615971520741376 posibilities.
Sometimes sharing a key is not practical, for example consider taking a credit card over the Web.
Suppose, however, that it were possible to find a cryptosystem for which
knowing e
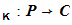 , and the general methodology used in its construction, did not lead to an
easy computation of d
, and the general methodology used in its construction, did not lead to an
easy computation of d
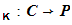 , then we could do the following.
, then we could do the following.
Secure One-Way Communication: (eg Web Form)
1. Publish e
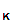 for the world to see. Tell the world that, if they want to communicate
securely with you, all they need to is apply e
for the world to see. Tell the world that, if they want to communicate
securely with you, all they need to is apply e
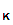 to the message before transmitting it. This because there is an acceptably
small chance of someone discovering d
to the message before transmitting it. This because there is an acceptably
small chance of someone discovering d
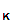 hence decoding there message.
hence decoding there message.
2. When I received the encrypted message apply d
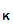 which, presumably only I know.
which, presumably only I know.
Secure Two-Way Communication:
Assume that we are dealing with a Cryptosystem such that
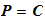
In addition to
d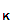 (e
(e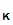 (M
))
(M
))
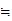 M, we have
e
M, we have
e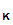 (d
(d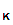 (C
))
(C
))
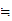 C for all C
C for all C
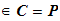 .
.
Given
d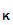 (),
it is also very hard to compute
e
(),
it is also very hard to compute
e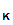 ().
().
Suppose that we have two people
P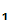 and
P
and
P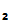 who want to communicate securely with each other. Each selects their own "one
way system", K
who want to communicate securely with each other. Each selects their own "one
way system", K
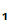 and K
and K
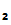 ,
from a Cryptosystem with the above listed properties .
,
from a Cryptosystem with the above listed properties .
P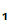 and
P
and
P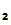 commmunicate as follows:
commmunicate as follows:
1.
P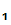 gives e
gives e
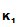 to
P
to
P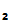 and
P
and
P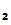 gives e
gives e
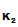 to
P
to
P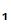 .
.
2. Suppose
P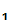 wants to send message M to
P
wants to send message M to
P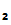 .
P
.
P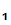 computes C
computes C
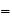 e
e
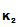 (d
(d
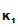 (M
)) and transmits it.
(M
)) and transmits it.
3.
P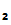 computes e
computes e
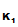 (d
(d
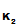 (C
))
(C
))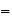 e
e
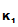 (d
(d
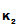 (e
(e
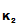 (d
(d
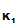 (M
))))
(M
))))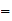 e
e
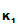 (d
(d
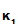 (M
))
(M
))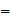 M.
M.
Why does this work?
P knows that the only person who can read the message is
P
knows that the only person who can read the message is
P , the owner of K
, the owner of K
 since, presumably
P
since, presumably
P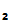 , is the only person who knows d
, is the only person who knows d
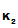 ().
().
P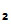 knows that
P
knows that
P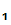 sent the message since, presumably
P
sent the message since, presumably
P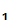 , is the only person who knows d
, is the only person who knows d
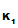 ().
We are implicitly assuming that the message
P
().
We are implicitly assuming that the message
P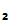
sees is meaningful.
1. Begin by choosing
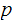 and
and
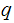 to be two very large prime numbers.
to be two very large prime numbers.
2. Next choose
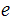 ,
,
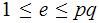 ,
such that
,
such that
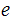 and
and
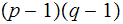 are relatively prime.
are relatively prime.
3. Referring to a topic we will cover , we can find
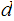 such that
such that
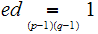 .
( ed = a(p-1)(q-1) + 1 ) Note that
.
( ed = a(p-1)(q-1) + 1 ) Note that
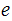 and
and
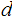 are "symmetric" for two way communication.
are "symmetric" for two way communication.
4. We will also need to know that for any M, M(p-1)(q-1)=1 mod pq
5. Here is RSA
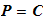 is the set of integers between
is the set of integers between
 and
and
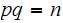 and relatively prime to
and relatively prime to
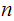 .
.
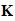 the keyspace, is the set of pairs
the keyspace, is the set of pairs
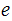 ,
,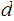 as above:
as above:
For each K
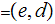 in
in
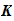 and all M
and all M
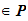 ,
e
,
e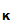 (M
))
(M
))
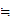 M
M
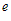 =C and
d
=C and
d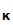 (C
)
(C
)
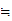 C
C
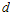
Note:
d
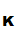 (e
(e
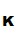 (M))
(M))
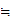 M
M
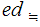 M
M
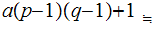 (M
(M
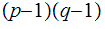 )
)
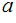 M
M
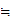 (1)
(1)
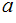 M
M
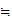 M
M
And
d
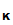 (e
(e
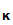 (M))=M.
(M))=M.
Example- Let
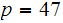 and
and
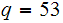 .
.
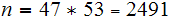
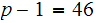 and
and
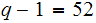 .
So
.
So
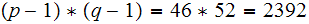 .
Choose
.
Choose
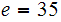 .
Note
.
Note
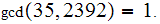
Somehow Compute
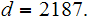
Suppose M
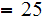
 Check
Check
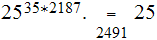

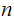 all we really need to do is find
all we really need to do is find
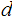 such that
such that
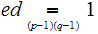 ,
so given,
,
so given,
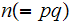 ,
is there a way to compute
,
is there a way to compute
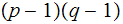 ?
?
The answer is that it is as "hard" to compute
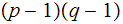 from
from
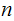 as it is to factor
as it is to factor
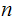 it self. Here is the argument.
it self. Here is the argument.
1. For the sake of clarity, set
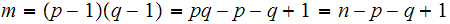 .
So if we know
.
So if we know
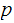 and
and
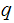 we can quickly compute
we can quickly compute
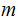 .
.
Next the important direction.
2. Suppose there was an easy way to compute
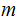 from
from
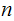 .
To factor
.
To factor
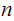 ,
we would then only have to solve the two simultaneous equations.
,
we would then only have to solve the two simultaneous equations.
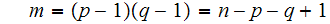
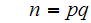
in two unknowns
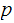 and
and
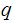 .
.
Solving the first equation for p gives.
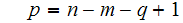
substituting this into the second equation gives.
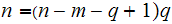
or
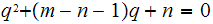 .
.
The quadratic formula does the rest.