A possible talk on this cycle for physics teachers (e.g. at the 2016 ISAAPT Fall meeting in Peoria IL) might have an outline of the form:
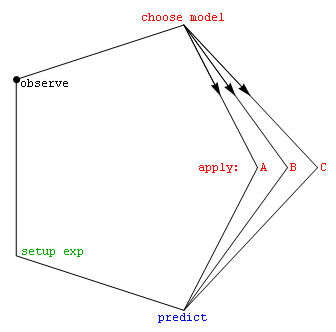
Note that this cyclic view of the scientific method (figure at right) avoids the true/false-hypothesis component of scientific method characterizations: It asks "Which concept set is most effective in a given situation?" rather than the binary-logic question "Is that assertion a perfect match to the world around?".
This approach also makes explicit the gestalt pattern-recognition problem, i.e. the fact that evolving concept-sets (and shifting paradigms) are key to guiding which aspects of future observations will make it at all into the record for downstream analysis. Finally, of course, one might see the cycle portrayed in the figure as a key element for models of scientific method as a continuously evolving physical process, as distinct from an activity with a beginning and an end.
Although physics courses have historically focused on "prediction strategy" rather than on other elements in the cycle, we begin here with observations, because in the "chicken or egg" problem it makes sense that the cycle began with input from our senses about goings-on in the world around. In what follows, we then proceed around the cycle, in the process introducing quite disparate elements of intro-physics content-modernization that are relevant to the changing world in which our students find themselves.
This usually involves taking some sort of data. Although it would be nice to imagine that we were recording the truth, the whole truth, and nothing but the truth, in fact the sensory-instruments and asked-questions that are used to take the data inevitably color the kinds of concepts that might serve to model what you find, as well as the data you have to work with.
Theory and practice here includes:
and what else?

To illustrate this we describe a Firefox app, inspired by our electron scattering studies of crystal lattice defect structure, designed to make sounds accessible (including Fourier phases not generally audible) in real time to YOUR neural-network for visual pattern recognition [1].
The key to phase-visualization over a wide dynamic range of intensities is to use pixel-brightness/saturation to represent the log-amplitude of a complex number, and pixel-hue to represent the Fourier phase. This method of using color images to display 2D arrays of complex numbers of course has many other uses in physics education, one of which is illustrated in the (lower left) digital darkfield panel of the electron optics simulator discussed below.
As shown in the figure at right, following musicians we lean toward "log-frequency vs. time spectrogram" formats, since they make frequency-ratios (like octaves) much easier to recognize. In this context, look for visual field guides to all kinds of sounds in the days ahead, as well as (hopefully) an improved path for folks with hearing impairments to enhance their expertise in both sound recognition and generation.
Given data, "What set of concepts is most helpful for putting it to use?" is perhaps the most difficult question of all to answer. One reason is that the choice of concepts to use in modeling processes is an open-ended question. Another reason is that models useful for predicting often are not easy to operate in reverse, i.e. the "inverse problem" is not easily or unambiguously solved.
Theory and practice here includes:
and what else?

To introduce the quantitative science of model-selection (which may be less familiar than parameter-estimation to academic physicists), we begin with something that is familiar: the now half-century old switch to the statistical approach (cf. Reif, Kittel and Kroemer, Stowe, Garrod, Schroeder, etc.) for teaching thermal physics in senior undergraduate (and later) courses. Although one might think of this as "entropy-first", it is unavoidable that in the years ahead we'll be seeing this (cf. [2]) as a "correlation-first" approach instead.
In that context we may want to carefully point out, even to conceptual-physics students via the expression #choices = 2#bits, the robust connection between surprisals (e.g. s≡ln2[1/p] in bits) and wide-ranging cross-disciplinary uses for "the second law" in statistical terms i.e. that correlations between isolated subsystems generally do not increase as time passes.
In the world of binary logic, surprisal gives practical meaning to the phrase "bits of evidence", while in the world of probabilities (0≤p≤1) it shows how to relate coin-tosses to decisions e.g. about games of chance and medical choices for a visceral feeling of what very small and very large odds mean. More importantly, it serves up a more general way to quantify available work (i.e. ordered energy from things like renewable and non-renewable sources), not to mention a way to understand the "kids on a playground" force behind heat flow (including systems with inverted population states).
For our purposes here, surprisal independently lies at the heart of parallel themes in the physical [3] and behavioral [4] sciences for choosing which models work best. The elegant Bayesian solution in both cases (albeit not always easy to quantify in practice) is simply to choose the model which is "least surprised" by incoming data. The shared basis for both approaches automatically addresses the more familiar reward for "goodness of fit", along with an Occam-factor penalty for model complexity e.g. through the number of free parameters involved. When there is no time for the formal mathematics, students might instead be encouraged to discuss which historical ideas in wide-ranging areas were surprised by new data, and what happened as a result.
I should also mention that, thanks to connections made by Claude Shannon and Ed Jaynes, surprisal as a correlation-measure fits nicely into the information age of both regular and quantum computers [5]. It further shows promise for helping us develop cross-disciplinary measures of community health [6], which focus on correlations that look in/out from skin, family and culture.
Obtaining predictions from one's collection of models is an evolving challenge in most fields. This is certainly true with most quantitative models, because the tools for obtaining and vetting predictions from a model (especially the former) are changing rapidly as the digital logic tools available to support those processes continue to change.
Theory and practice here includes:
and what else?

The metric-equation's synchrony-free "traveler-point parameters", namely proper-time τ, proper-velocity w ≡ dx/dτ, & proper-acceleration α, are useful in curved spacetime because extended arrays of synchronized clocks (e.g. for local measurement of the map-time t increment in Δx/Δt) may be hard to find. These same parameters can better prepare intro-physics students for their everyday world, as well as for the technological world e.g. of GPS systems where differential aging must be considered explicitly. However, some old ways of teaching may need minor tweaks.
For instance, high-school students in AP Physics are sometimes taught that centrifugal force is fake, even though:
In fact Einstein's general relativity revealed that Newton's laws work locally in all frames (including accelerated-frames in curved-spacetime), provided that we recognize geometric forces like gravity and inertial forces [7], which often link to differential aging (γ≡dt/dτ) with "well-depths" (e.g. in rotating habitats, accelerating spaceships, and gravity on earth) directly connected to (γ-1)mc2. Moreover, the net proper-forces [8] that our cell-phones measure (which are generally not rates of momentum change) are "frame-invariant" much as is proper-time, making curved spacetime (like that we experience on earth's surface) a bit simpler to understand than we might have imagined from a "transform-first" course in special relativity.
Since this insight came into focus a century ago, perhaps it is appropriate (as is already happening with the increasing textbook use of proper-time) to tell physics students in general, and not just folks who've become grad-students with a theoretical bent, that traveler-point parameters (as complement to familiar variables like coordinate-velocity) can help us both understand and predict. At the very least perhaps it's a good excuse to say that time elapses differently on all clocks, according to both position and rate of travel, but that we appoximate by saying that t represents time-elapsed on synchronized clocks connected to the yardsticks which define our frame of reference.
To give you a taste of the traveler-point variable notation in classic terms, imagine
a traveler with book-keeper coordinates x[t] seen from the vantage point of a
"free-float" or inertial frame in flat spacetime
with no geometric forces, so that the equation of motion
DUλ/dτ - ΓλμνUμUν
= dUλ/dτ in the form "proper + geometric = observed" predicts
that the net proper-force
ΣFo alone will be 3-vector mα (e.g. to moving charge q a Lorentz force like
qFλβUβ =
qγ{E•v/c, E+v×B} becomes spacelike yielding a 3-vector force
qE' = q(E||w+γE⊥w+w×B) which
is purely electrostatic), where m is
frame-invariant rest-mass and α is "frame-invariant" proper-acceleration (with a
traveler-defined 3-vector direction).
Then differential-aging factor γ ≡ dt/dτ =
√1+(w/c)², proper-velocity w
≡ dx/dτ = γv where
coordinate-velocity v ≡ dx/dt, momentum
p = mw, kinetic energy K = (γ-1)mc2,
rate of energy change dK/dτ = mα•w, and
the rate of momentum change is dp/dτ =
mα+(γ-1)mα
For example in nanoscience, this generally involves synthesis, preparation of specimens for analysis, as well as the design, operation, and funding of instrumentation for finding out what you either found, or created.
Theory and practice here includes:
and what else?

Although general multi-slice calculations remain too slow, web-browsers on many platforms now make possible real-time single-slice (strong phase/amplitude object) simulation, with live image, diffraction, image power-spectrum, and darkfield-image modes, including specimen rotation e.g. for atomic-resolution images with specimens having several tens of thousands of atoms [9]. Moreover, a wide range of qualitative phenomena emerge that include diffraction-contrast effects associated with thickness, orientation changes, and defect strain.
Hence students with no math background can get a visceral feel for the way 2-D lattice-projections, diffraction-patterns, image power-spectra, aperture size/position, and darkfield images relate to a specimen's structure & orientation, as well as microscope contrast-transfer, well before access to a real electron microscope is available. Our JS/HTML5 platform even shows promise for the construction of procedurally-generated (in effect, arbitrarily large) worlds from the atomic-scale up, to be explored on-line.
The caveat is that we are accessing the nanoworld using simulated electron optics, which involves unfamiliar contrast-mechanisms perhaps accessible only with help from a "physics filter". As a result developing a knack for experimental setups, e.g. to focus and astigmate the lenses, orient the object being examined, and decide what signals to record via the position of apertures, creates a very robust physics-rich (and realistic) challenge for prospective nanoexplorers. As you might imagine, these skills may prove useful in a variety of job settings for students downstream.
[1] Stephen Wedekind and P. Fraundorf (Sept 2016) "Log complex color for visual pattern recognition of total sound" (patent pending) Audio Engineering Society Convention 141, paper 9647 AES library mobile-ready link.
[2] James P. Sethna (2006) Entropy, order parameters and complexity (Oxford U. Press, Oxford UK) (e-book pdf).
[3] Phil C. Gregory (2005) Bayesian logical data analysis for the physical sciences: A comparative approach with Mathematica support (Cambridge U. Press, Cambridge UK).
[4] Burnham, K. P. and Anderson D. R. (2002) Model selection and multimodel inference: A practical information-theoretic approach, Second Edition (Springer Science, New York).
[5] Seth Lloyd (1989) "Use of mutual information to decrease entropy: Implications for the second law of thermodynamics", Physical Review A 39, 5378-5386 (link).
[6] P. Fraundorf (2017) ''Task-layer multiplicity as a measure of community health'', hal-01503096 working draft on-line discussion.
[7] cf. Charles W. Misner, Kip S. Thorne and John Archibald Wheeler (1973) Gravitation (W. H. Freeman, San Francisco CA).
[8] P. Fraundorf (2017) "Traveler-point dynamics", hal-01503971 working draft on-line discussion webpage.
[9] P. Fraundorf, Stephen Wedekind, Taylor Savage and David Osborn (2016) "Single-Slice Nanoworlds Online", Microscopy and Microanalysis 22:S3, 1442-1443 Cambridge hal-01362470 pdf mobile-ready link.