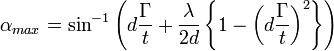Lattice fringe visibility

Although more than one contrast mechanism can create them, lattice fringes are normally made visible by electron phase contrast in a conventional high resolution electron microscope (HRTEM). This contrast maps high energy electron deBroglie phase shifts at the exit surface of the specimen by recording intensity variations that result from wave interference downstream of the specimen e.g. at "Scherzer defocus". The phenomenon is made even more remarkable since beam currents are so low that to pull this off individual electrons must interfere with themselves.

Here is our J Appl Phys paper. Two other papers from our group on this subject may be found here and here. Some interactive 3D maps may be found here. I'll list some of the many applications described by us and others shortly. Wiki sections on Icosahedral twins, and on Nanocylinder aligned crystals crystals, are only a taste. Additional clues may be found on our page about image-based crystallography.

Fringe-visibility/bend-contour rocking curves

Speaking of the visibility of lattice fringes as a function of specimen orientation in a transmission electron microscope, the expression for fringe visibility half-angle in kinematic approximation looks like:

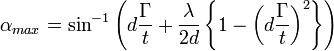$\alpha_{max}=\sin^{-1}\left(d\frac{\Gamma}{t}+\frac{\lambda}{2d}\left\{1-\left(d\frac{\Gamma}{t}\right)^2\right\}\right)$ .

In the expression above, d is the spacing of the lattice planes, t is the crystal thickness, λ is the wavelength of the electrons, and Γ is a “visibility factor” on the order of 1 that empirically accounts for the signal-to-noise ratio in the method used to detect fringes.

Replacing Γ/t with deviation parameter or excitation error s in the above equation, one can solve for deviation parameter in terms of off-edge angle α to get:

$s[\alpha]=\left|{\frac{\sqrt{1-2(\lambda/d)\sin{\alpha}+(\lambda/d)^2}-1}{\lambda}}\right|$ .

The Fourier shape transform of a spherical crystal in three dimensions, in terms of spatial frequency g and sphere diameter t, may be written:

$\Xi[g] = \frac{\sin{\pi g t}- \pi g t \cos{\pi g t}}{2 \pi^2 g^3}$ .

Consider a lattice plane canted by angle α radians from the edge-on position along the electron-beam direction. Since all reciprocal lattice spots will be convolved with the shape transform, the intensity of Bragg scattering from the brightfield (unscattered beam) image can be estimated by adding amplitudes (in the coherent kinematic scattering case) from both sides of the lattice plane by adding Ξ[s] values for deviation s[α] evaluated at ±α. The result is illustrated in the figure below.

Bend contour and lattice fringe visibility as a function of specimen thickness and beam tilt.

Great circle band intersection areas

An interesting related problem: What's the area of the orientation sphere subtended by the intersection between two such bands, say each of half-angle α, since this relates to the probability of encountering lattice cross-fringes in a collection of randomly-oriented crystals. Consider first the case of equal bands intersecting at right angles. We are interested in σ₂, twice the area σ₁ of a single intersection, because great-circle bands intersect twice on opposing sides of the orientation unit sphere.

For α<π/4 a lovely equation for the exact value of the intersection solid angle has been discovered by Dr. Jon Bailey, to wit:

$\sigma_1 = 8 \sum\limits_{n = 1}^\infty {\frac{{( - 1)^{n + 1} \sin[\alpha]^{2n} }}{{n!}}} F[n]\prod \limits_{k = 1}^n {(\frac{3}{2} - k)} = 4 \alpha^2 + \frac{2}{9} \alpha^6 + \frac{8}{45} \alpha^8 +$ ...,

where hypergeometric function F[n] is

$F[n] \equiv \sum\limits_{m = 0}^{n-1} \frac{(n-1)!}{m!(n-1-m)!} \frac{1}{2m+1}$ .

For α>π/4, upper and lower visibility zones connect leaving only four circular "cross-free caps". Hence σ₁ then becomes 2π(2sin[α]-1).

These observations show that an excellent approximation for small angles is σ₂ ~ 2(2α)², i.e. twice the area one would calculate for a flat square of side 2α. The approximation error (from above) is to first order (4/9)α⁶, which is still below 0.5% when bandwidth 2α is a radian. When crossing bands have half-angles of α₁ and α₂, and they intersect at an angle of φ radians, the flat polygon estimate becomes

$\sigma_2 \cong \frac{2 (2 \alpha_1)(2 \alpha_2)}{\sin[\phi]}$ .

Intersection areas of multiple bands, e.g. for analysis of fringe visibility in 10-crystal icosahedral twins, remain an active area of inquiry. If you like thinking about geometry problems like this, leave a note here.