
Papers by our group on digital darkfield applications include this, this, this, this, this, and Martin's thesis. Rich Leapman (US editor of J. Microscopy and NIH physicist) expressed some interest in an article for their readers, although we might also want to work on an article accessible to the mathematical harmonic analysis community. ImageJ plugins that we've written for this type of work may be found here.


Although mutual information is a multi-moment measure of correlation, second-moment measures lie at the heart of exciting pattern-recognition tools in mathematical harmonic analysis (like wavelet theory) which reside between direct and reciprocal space. A new frontier for their application lies in detective work on atom-resolution images. The notes here connect these new developments to electron-optical "analog computing" strategies that have been in use for decades.
Using Cartesian coordinates in 2D and a common bandwidth (or frequency scale parameter) Δf for each direction, the windowlet transform of an input function s[x,y] (e.g. a deBroglie wave at the 2D exit surface of a physical specimen) is represented by:
Note that the output ψ is generally complex even if the input signal s is real. Here x={x,y} is a direct-space shift vector, and fo is a frequency or reciprocal-space shift vector. Suppose that the kernel h[ξ,η] can be further written, in terms of dimensionless 2D variables ξ in direct-space and η in reciprocal space, as the product wg of a window function w[ξ] and the Fourier modulation function g[ξ,η] = e-2πiξ·η. In that case the Fourier transform of the windowlet becomes:
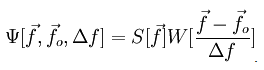
Here of course W and S are the Fourier transforms, respectively, of w and s.
Finally a square Shannon (or Littlewood-Paley) window in frequency space (this corresponds to a square aperture in the back-focal or transverse-momentum plane of an electron optical system) might be written as W[ηx,ηy] = rect[ηx] rect[ηy] where
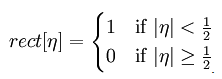
In direct space, the shape-transform of this aperture is a 2D sinc-window of the form:
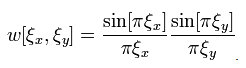
Although square or rectangular sinc-windowlets are useful when one wishes to comprehensively tile reciprocal space (wavelets per se typically use a hierarchy of 2×2 tilings), circular back-focal plane apertures are more common experimentally. These give rise in direct space to Airy (Bessel function) rather than sinc windows. The convergence properties of Airy windows are more isotropic.
When |fox|<Δf/2 and |foy|<Δf/2, microscopists who use electron-optical methods to do this calculation for an exit wave think of the map of intensity ψ*ψ as a brightfield image (exclusively so when illumination is parallel) because it includes the unscattered beam or DC peak. Regions in the image without scatterers are therefore bright.
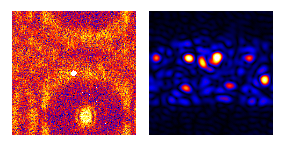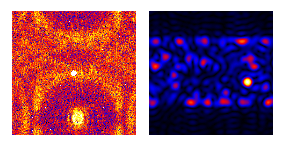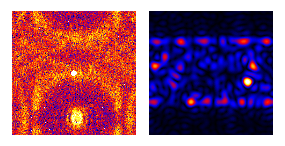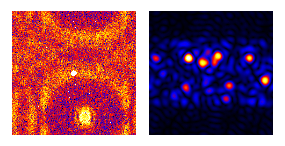
Conversely when the frequency-space aperture excludes the unscattered beam, microscopists call the ψ*ψ map a darkfield image. Only objects with periodicity in bandwidth Δf, centered on the frequency shift vector fo of this square aperture, light up in the ψ*ψ field. The corresponding phase maps of arg[ψ] = -i ln[ψ/|ψ|], on the other hand, contain very precise information on vector periodicity-displacement and hence strain tensors in projection. For example, maps of picometer-scale strain in atomic lattices have been made via these transforms, using microscopes with point-resolutions only in the 0.2 nanometer range.
The above windowlet is a direct-reciprocal inversion (in 2D) of the short-time Fourier transform. It has zero mean and is square integrable. Its transform also meets (at least for parallel illumination) the wavelet-decomposition admissibility condition in the darkfield case i.e. when the frequency window does not include the zero-frequency point or DC peak. The weak point of this decomposition is that support in direct space is not compact but instead exhibits sinc-system convergence, proportional to 1/x as x→∞ i.e. at the slow end of the Haar to sinc continuum.