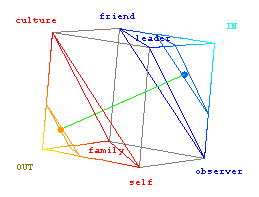
An interesting visualization for a set of six probabilities (or other positive numbers which sum to 1) involves a pair of linked triangles (2-simplexes) embedded in opposing corners of a cube. The example below is labeled to document the fractional allocation of an individual's attention across niche levels on six different size scales.

The red triangle elaborates on the individual's distribution of focus across levels defined as inward-looking from three physical boundaries: skin, gene pool edge, and meme pool edge. The inward-looking simplex of an individual (the orange triangle here) will lie parallel to the red plane, but shrink along a line toward the OUT-labeled cube corner as the balance of an individual's attention shifts away from these inward-looking niche layers.
The blue triangle does the same for focus looking outward from the same three physical boundaries. In that case the individual's triangle (blue-green) shrinks along a line toward the IN-labeled cube corner as the individual's balance of attention shifts toward the niche layers whose focus is inward from those three physical boundaries.
The figure above loads with an informative view of the cube down its IN-OUT body diagonal, although you can rotate your view with the mouse as desired. As in the earlier figure, an individual's state is specified by two dots on a pair of parallel planes separated by 2/3 of the cube's body diagonal. In particular the orange and blue-green dots above, connected by a green line, denote an otherwise balanced individual who is preoccupied with knowledge acquisition at the expense of self care. You can see this in that the orange dot is displaced from center away from the smallest-scale "self" vertex, while the blue-green dot is displaced from center toward the largest-scale "observer" vertex. Since the particular displacements also shift the balance to the outward-looking (blue) simplex, the blue-green triangle has also become larger than the orange one. The result of these shifts is a niche level multiplicity of 5.48 out of the 6 possible if all six niches are given equal emphasis. How does the dual dsimplex for your niche connections compare?
The figure below compares the niche connections above (illustrated in the upper right quadrant below) to a completely balanced probability assignment (upper left quadrant below), and to two other systems. Basically, imbalance develops as the points drift toward the edges or corners of the triangles associated with those two dots. If this drifting also results in a change in balance between inward and outward focus, the sizes of these two triangles also change.
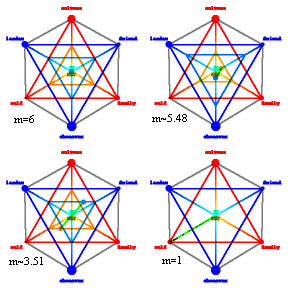
For example, the m=6 state in the upper left has orange and blue-green triangles which are equal in size, and dots located at the center of each (as far a possible from each edge). The m=5.48 state in the upper right has dots a bit off center, and a blue-green triangle a bit larger than the orange one. The latter represents a bias toward outward focus (in this case e.g. scholarly observation). The m less than 4 state in the lower left has dots which have moved to the edges of each triangle. In this case basically the meme-pool boundary niches (largest in scale, and probably latest in evolutionary time) have been turned off. This might for example represent a primitive form of community lifeform in which social communication and learning by non-molecular means plays little role. However, in this case we've kept the balance between inward and outward focus intact. The lower right panel represents an isolated individual focussed only on self-care. In this case, the blue-green (out-focus) triangle has shrunk to a point, while the orange dot has moved to the self-only corner of the orange triangle, which has grown to be isomorphic with the red.
If you prefer something with fewer square corners, try this octahedral version of the dual simplex model above with m~5.48. Again the spacing between triangles for the individual is fixed. At either extreme of the in/out or nurture/explore continuum for an individual, these triangles mark the corners of a regular tetrahedron, while at the balance (m=6) point they mark the corners of a regular octahedron. Is your dual simplex more octahedral or more tetrahedral? Niche connections for most folks will take the shape of a non-regular octahedron somewhere on the continuum between. Also, we've drawn grey guide lines for the larger "hour glass" frame only between endpoints which are adjacent in scale size, or (for symmetry) at opposite ends of the size scale. Both figures below can be rotated in 3 dimensions if you like.