The 0th Law of Gambling Theory
(oops, Thermodynamics)

Where might we expect to find a conserved quantity X
which has been randomly shared between systems for so long that
prior information about the whereabouts of X is irrelevant?
In other words, where is X likely to be after equilibration?

The most likely partitioning of X is
that which can happen in the most ways, at which point
all sub-system uncertainty slopes dS/dX become equal
lest the flow of X to higher slope sub-systems persist.
Here accessible states Ω is the number of ways
a (sub-)system might accomodate quantity X, and
uncertainty or entropy S ≡ k ln Ω, where k is
{1, 1/ln2, 1.38×10-23} for S in {nats, bits, J/K} respectively.

Ω≡eS/k (#choices=2#bits), and X flows randomly toward larger dS/dX.

Example: Energy Sharing & Equipartition

When energy E is the quantity randomly shared between systems,
the uncertainty slope dS/dE is the reciprocal temperature or coldness 1/T.
For many phases over some temperature range, Ω ∝ EνN/2,
where N is the number of molecules and ν is the number of
degrees freedom or ways to store thermal energy per molecule.
Solving this for dS/dE gives the equipartition theorem E/N = (ν/2)kT.

Example: Volume Sharing & the Ideal Gas Law

When volume V is the quantity randomly shared between systems,
the uncertainty slope dS/dV is the free expansion coefficient
equal to (dS/dE)(dE/dV)=(1/T)(Fdx/Adx) = P/T.
For ideal (low density) gases, Ω ∝ VN.
Solving this for dS/dV gives the ideal gas equation of state PV = NkT.

Example: Particle Sharing & Mass Action

When number of particles N is randomly shared between systems,
the uncertainty slope dS/dN is the chemical affinity α ≡ -μ/kT.
For many systems, Ω ∝ ζN/N! so that dS/dN = ln[ζ/N]
where ζ is the # of independent states accessible to a given molecule.
If a molecule has stoichiometric coefficient b in a reaction,
at equilibrium the b-weighted sum of slopes goes to zero.
Hence, the product of (ζ/N)b for each reactant goes to one.

The 1st Law of Thermodynamics

Random energy movement predicted by the 0th law above is called heat flow.
The 1st law says that the total energy change dE equals heat δQin minus work δWout.
Here the imperfect differential δWout = PdV + other forms of work.

The 1st law, equipartition, and PV=NkT, can be used to predict
changes to an ideal gas under various "constraints".
Isobaric changes hold dP to zero (pressure constant).
Isothermal changes hold dT to zero (temperature constant).
Isochoric changes hold dV to zero (volume constant).
Adiabatic changes hold δQ (heat transfer) to zero.

Integral heat capacity E/kT is the exponent of energy
in the expression for multiplicity Ω, while
the differential no-work (e.g. constant volume) heat capacity
CV is the multiplicity exponent of temperature.
At constant pressure, enthalpy H≡E+PV plays the role of E,
while heat capacity at constant pressure is CP=CV+PdV/dT.
Heats of fusion/vaporization associated with bound states
yield first-order phase changes with heat capacities unbound.

The 2nd Law of Thermodynamics

The 2nd law says that entropy δS = δQin/T - δImutual + δSirr where δSirr≥0.
This follows from the uncertainty slope equations above,
assuming that our uncertainty about the state of an isolated system
(i.e. one for which dE=0 and dV=0) can only increase as time goes on.

Isentropic changes hold δS (entropy change) to zero.
Reversible changes hold δSirr to zero.
Also note that extensive variables like E and V add up system contents
while intensive variables like T and P can be measured from point to point.

Steady State Engines

Engines process outside energy via cyclic alterations of their own state.
Since their own state cycles, the world outside
is where energy-form and correlation changes reside.

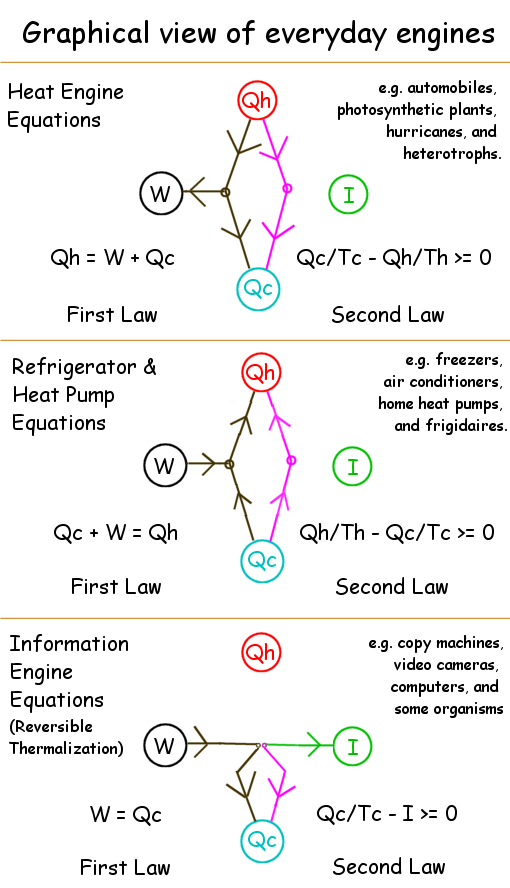
1st Law: Heat_IN + Work_IN = Heat_OUT + Work_OUT
2nd Law: Uncertainty_INCREASE - Correlation_INCREASE = NetSurprisal_LOST
where Uncertainty_INCREASE = Qout/Tout - Qin/Tin,
and NetSurprisal_LOST is always greater than or equal to zero.

A device for cooling hot water is discussed here,
while the role of reversible thermalization
in the development of correlation-based complexity
(e.g. on our planet) is illustrated below.


(Left) Life's Energy Flow: The top half represents
some of the primary processes involved with energy flow,
while the bottom half illustrates
significant physical repositories for life's energies,
and paths for conversion of energy (and net surprisal)
from one form to another.
(Right) Life's Stores of Availability:
Horizontal bars represent inward-looking correlations,
while vertical bars represent outward-looking correlations.
This breakdown seems to work reasonably well
to categorize by domain both the types of correlations found,
and the types of codes (e.g. genetic or memetic replicators)
used to help maintain them.

Below find a concept map which ties some of these
things together. Click here for a live version.